
【题目】如图,△ABC是等边三角形,BC=2![]() .点P从点A出发沿沿射线AB以1
.点P从点A出发沿沿射线AB以1![]() 的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1
的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1![]() 的速度运动,连结BE、EQ.设点P的运动时间为t(
的速度运动,连结BE、EQ.设点P的运动时间为t(![]() ).
).

(1)求证:△APE是等边三角形;
(2)直接写出CE的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点P在边AB上,且不与点A、B重合时,求证:△BPE≌△ECQ.
(4)在不添加字母和连结其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.
【答案】(1)见解析;(2)2-t或t-2;(3)见解析;(4)当t=1时,图中有5个等腰三角形;当t=4时,图中有4个等腰三角形
【解析】
(1)根据等边三角形的性质可得∠A=∠ABC=∠ACB =60°,根据平行线的性质可得∠APE=∠ABC=60°,∠AEP=∠ACB=60°,再利用等边三角形的判定即可得证;
(2)由(1)可得AE=AP=t,分E没过C点与过C点两种情况进行解答即可;
(3)△ABC与△APE都是是等边三角形,利用等边三角形的性质易证BP=EC,∠BPE=∠ECQ=120°,再通过“边角边”证明△BPE≌△ECQ即可;
(4)当P在AB的中点,即t=1时,图中有5个等腰三角形;当P点在AP=2AB,即t=4时,图中有4个等腰三角形.
(1)∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB =60°,
∵![]() ,
,
∴∠APE=∠ABC=60°,∠AEP=∠ACB=60°.
∴△APE是等边三角形;
(2)∵△APE是等边三角形,
∴AE=AP=t,
当E点没过C点时,AE=2﹣t;
当E点过了C点时,AE=t﹣2;
(3)∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∵△APE是等边三角形,
∴AP=PE=AE,∠APE=60°.
∴AB-AP=AC-AE,∠BPE=∠ECQ=120°,
∴BP=EC,
∵AP=CQ=t,
∴PE=CQ,
∴△BPE≌ECQ(SAS);
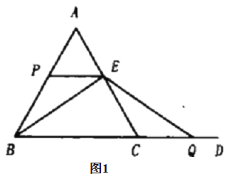
(4)如图1,当t=1时,图中有5个等腰三角形:△ABC,△APE,△PBE,△CQE,△EBQ;
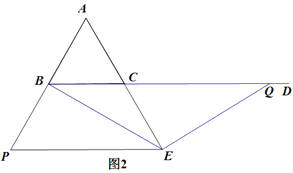
如图2,当t=4时,图中有4个等腰三角形:△ABC,△APE,△CBE,△EQB.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E. 已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)求证:DE=CF
(2)求BC+DE的值
(3)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育,警钟长鸣”,为此某校从14 000名学生中随机抽取了200名学生就安全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图甲).
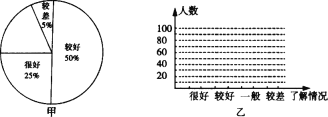
(1)补全扇形统计图,并计算这200名学生中对安全知识了解“较好”、“很好”的总人数;
(2)在图乙中,绘制样本频数的条形统计图;
(3)根据以上信息,请提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.
(1)若想围得花圃面积为192cm2,求x的值;
(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:

经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,面积是 (写成多项 式乘法的形式);

(3)比较图1、图2 阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算:(a+b-2c)(a-b+2c).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com