Question

【题目】已知AM∥BN，AE平分∠BAM，BE平分∠ABN，

（1）求∠AEB的度数．

（2）如图2，过点E的直线交射线线AM于点C，交射线BN于点D，求证：AC+BD＝AB；

（3）如图3，过点E的直线交射线线AM的反向延长线于点C，交射线BN于点D，AB＝5，AC＝3，S△ABE﹣S△ACE＝2，求△BDE的面积．

Answer 1

【答案】(1) ∠AEB=90°；（2）见解析；（3）8.

【解析】

（1）根据平行线的性质得到∠BAM+∠ABN=180°，根据角平分线的定义得到∠BAE=∠BAM，∠ABE=∠ABN，于是得到结论；

（2）在AB上截取AF=AC，连接EF，证明△ACE≌△AFE，根据全等三角形的性质得到∠AEC=∠AEF，然后证明△BFE≌△BDE，得到BF=BD，等量代换即可得到结论；

（3）延长AE交BD于F，根据等腰三角形的性质得到AB=BF=5，AE=EF，根据全等三角形的性质得到DF=AC=3，设S△BEF=S△ABE=5x，S△DEF=S△ACE=3x，根据S△ABE-S△ACE=2，即可得到结论．

解：（1）∵AM∥BN，

∴∠BAM+∠ABN=180°，

∵AE平分∠BAM，BE平分∠ABN，

∴∠BAE=∠BAM，∠ABE=∠ABN，

∴∠BAE+∠ABE=（∠BAM+∠ABN）=90°，

∴∠AEB=90°；

（2）在AB上截取AF=AC，连接EF，

在△ACE与△AFE中， ，

∴△ACE≌△AFE，

∴∠AEC=∠AEF，

∴∠AEB=90°，

∴∠AEF+∠BEF=∠AEC+∠BED=90°，

∴∠FEB=∠DEB，

在△BFE与△BDE中， ，

∴△BFE≌△BDE，

∴BF=BD，

∵AB=AF+BF，

∴AC+BD=AB；

（3）延长AE交BD于F，

∵∠AEB=90°，

∴BE⊥AF，BE平分∠ABN，

∴AB=BF=5，AE=EF，

∵AM∥BN，

∴∠C=∠EDF，

在△ACE与△FDE中，，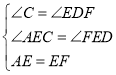

∴△ACE≌△FDE，

∴DF=AC=3，

∵BF=5，

∴设S△BEF=S△ABE=5x，S△DEF=S△ACE=3x，

∵S△ABE-S△ACE=2，

∴5x-3x=2，

∴x=1，

∴△BDE的面积=8．