
【题目】在正方形![]() 中,连接
中,连接![]() ,
,![]() 为射线
为射线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),连接
不重合),连接![]() ,
,![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
提出问题:当点![]() 运动时,
运动时,![]() 的度数是否发生改变?
的度数是否发生改变?
探究问题:
(1)首先考察点![]() 的两个特殊位置:
的两个特殊位置:
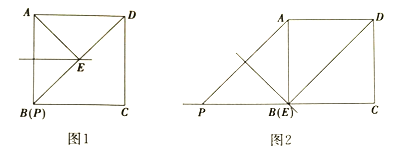
①当点![]() 与点
与点![]() 重合时,如图1所示,
重合时,如图1所示,![]() ____________
____________![]()
②当![]() 时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
(2)然后考察点![]() 的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)
的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)

(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图3和图4中任选一个进行证明;若不成立,请说明理由.
【答案】(1)①45;②不变化;(2)成立;(3)详见解析.
【解析】
(1)①②根据正方形的性质、线段的垂直平分线的性质即可判断;
(2)画出图形即可判断,结论仍然成立;
(3)如图2-1中或2-2中,作作EF⊥BC,EG⊥AB,证![]() 得∠AEG=∠PEF.由∠ABC=∠EFB=∠EGB=90°知∠GEF=∠GEP+∠PEF=90°.继而得∠AEP=∠AEG+∠GEP=∠PEF+∠GEP=90°.从而得出∠APE=∠EAP=45°.
得∠AEG=∠PEF.由∠ABC=∠EFB=∠EGB=90°知∠GEF=∠GEP+∠PEF=90°.继而得∠AEP=∠AEG+∠GEP=∠PEF+∠GEP=90°.从而得出∠APE=∠EAP=45°.
解(1)①当点P与点B重合时,如图1-1所示:
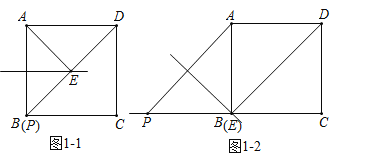
∵四边形ABCD是正方形,
∴∠APE=45°
②当BP=BC时,如图1-2所示,①中的结论不发生变化;
故答案为:45°,不变化.
(2) (2)如图2-1,如图2-2中,结论仍然成立;

故答案为:成立;
(3)证明一:如图所示.
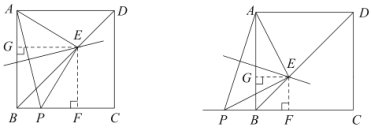
过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
∵点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
∴![]() .
.
∵四边形![]() 为正方形,
为正方形,
∴![]() 平分
平分![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
证明二:如图所示.
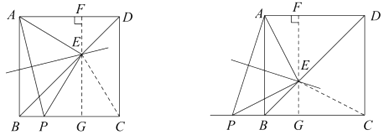
过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
∴![]() .
.
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
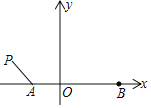
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣1,0),点B的坐标为(2,0),点P为线段AB外一动点且PA=1,以PB为边作等边△PBM,则当线段AM的长取到最大值时,点P的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
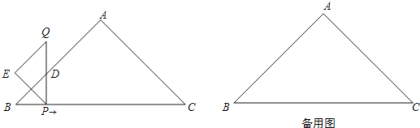
【题目】如图,在Rt△ABC中,AB=AC=4![]() .一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
(1)在整个运动过程中,设△ABC与△PQE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(2)当点D在线段AB上时,连接AQ、AP,是否存在这样的t,使得△APQ成为等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由;
(3)当t=4秒时,以PQ为斜边在PQ右侧作等腰直角三角形PQF,将四边形PEQF绕点P旋转,PE与线段AB相交于点M,PF与线段AC相交于点N.试判断在这一旋转过程中,四边形PMAN的面积是否发生变化?若发生变化,求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围;若不发生变化,求出此定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
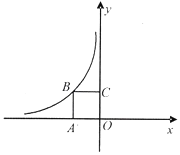
【题目】如图,正方形OABC的面积为4,点O为坐标原点,点B在函数y![]() (k<0,x<0)的图象上,点P(m,n)是函数y
(k<0,x<0)的图象上,点P(m,n)是函数y![]() (k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F.
(k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F.
(1)设矩形OEPF的面积为S1,求S1;
(2)从矩形OEPF的面积中减去其与正方形OABC重合的面积,剩余面积记为S2.写出S2与m的函数关系式,并标明m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com