练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
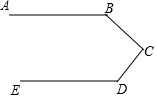
    14．如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=130°，∠D=120°，则∠C的度数为（　　）
    A．120°B．110°C．140°D．90°

    分析 过点C作CF∥AB，由平行线性质可得∠B，∠D，∠BCF，∠DCF的关系，进而求得∠C．

    解答 解：如图所示：过点C作CF∥AB．

    ∵AB∥DE，
    ∴DE∥CF；
    ∴∠BCF=180°-∠B=50°，∠DCF=180°-∠D=60°；
    ∴∠C=∠BCF+∠DCF=110°．
    故选：B．

    点评 本题主要考查了两直线平行，同旁内角互补的性质，解题时需要作辅助线求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届山东省淄博市（五四学制）九年级下学期第一次月考数学试卷（解析版） 题型：解答题

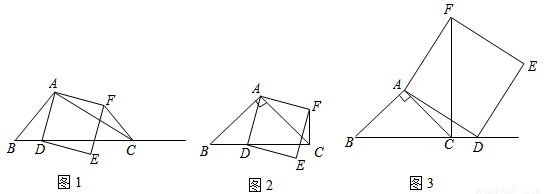
    在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．如果AB=AC，∠BAC=90o，

    （1）当点D在线段BC上时（与点B不重合），如图2，线段CF 、BD所在直线的位

    置关系为 __________，线段CF 、BD的数量关系为 ；

    （2）当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2017届山东省济南市天桥区九年级学业水平考试第一次模拟数学试卷（解析版） 题型：解答题

    (本小题满分9分)

    如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C(3，0)，D(3，4)，E(0，4)．点A在DE上，以A为顶点的抛物线过点C，且对称轴x＝1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．

    （1）直接写出点A坐标，并求出该抛物线的解析式．

    （2）在图1中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？

    （3）在图2中，若点P在对称轴上从点B开始向点A以2个单位/秒的速度运动，过点P作PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．一只蚂蚁沿着数轴从表示$\frac{1}{5}$的点爬到表示$\frac{4}{5}$的点，它经过的表示分数的点有（　　）
    A．0个B．2个C．4个D．无数个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

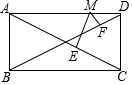    10．如图，在矩形ABCD中，AB=5，AD=12，M是AD上异于A和D的任意一点，且ME⊥AC于E，MF⊥BD于F，则ME+MF为（　　）
    A．$\frac{60}{13}$B．$\frac{30}{13}$C．$\frac{15}{13}$D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，已知AB∥CD，∠A=70°，则∠1的补角的度数是（　　）
    A．70°B．100°C．110°D．130°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．简便计算．
    （1）4892-487×491；
    （2）$\frac{1}{4}$×6.162-6.16×2.08+4×1.042．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．已知平面直角坐标系内的一点P（2，-3），则点P到x轴的距离是（　　）
    A．2B．-3C．-2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．在平面直角坐标系中，把直线y=2x向左平移1个单位长度，平移后的直线解析式是y=2x+2．

    查看答案和解析>>

    同步练习册答案