
【题目】将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.



图1 图2 图3
【答案】见解析
【解析】利用轴对称的知识找出等解即可进行推理判断.
解:当C′点落在CA和CB之间(如图2)时,∠1+∠3=2∠2;
当C′落在CB、CA的同旁(如图3)时,∠1-∠3=2∠2;
对于图2证明如下:
连结CC’,如图4所示,
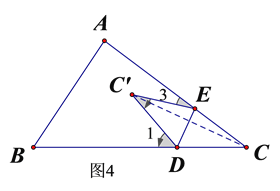
∵⊿EC’D是由⊿ECD翻折得到的,
∴⊿EC’D≌⊿ECD,由此得EC=EC’,DC=DC’,∠EC’D=∠ECD,
∴∠EC’C=∠ECC;∠DC’C=∠DCC,
∵∠1=∠DC’C+∠DCC’ ,∠3=∠EC’C+∠ECC’ ,
∴∠1+∠3=∠DC’C+∠DCC’ +∠ EC’C+∠ECC’=2∠DC’C+2∠ EC’C =2(∠DC’C+∠ EC’C)= 2∠2;
∴∠1+∠3=2∠2;
对于图3证明如下:
设AC与DC’在⊿ABC内部所夹角为∠4,如图5所示,
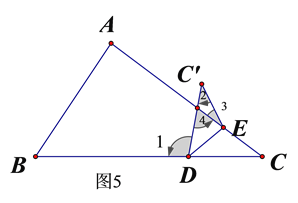
则有∠1=∠C+∠4,∠4=∠3+∠2,
又由翻折得:∠2=∠C,
∴∠1=∠2+∠3+∠2=∠3+2∠2,
∴∠1-∠3=2∠2.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.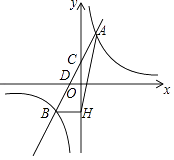
(1)求一次函数和反比例函数的解析式;
(2)求△ABH面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写理由:
已知:如图,ABC是直线,∠1=115°,∠D=65°.
求证:AB∥DE.

证明:∵ABC是一直线,(已知)
∴∠1+∠2=180°( )
∵∠1=115°(已知)
∴∠2=65°
又∵∠D=65°(已知)
∴∠2=∠D
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出ΔAPC≌ΔAPD.的是( )

A. BC=BD. B. ∠ACB=∠ADB. C. ∠CAB=∠DAB D. AC=AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,拋物线y=﹣ ![]() x2
x2 ![]() x与x轴交于O,A,点B在抛物线上且横坐标为2.
x与x轴交于O,A,点B在抛物线上且横坐标为2.
(1)如图1,△AOB的面积是多少?
(2)如图1,在线段AB上方的抛物线上有一点K,当△ABK的面积最大时,求点K的坐标及△ABK的面积;
(3)在(2)的条件下,点H 在y轴上运动,点I在x轴上运动.则当四边形BHIK周长最小时,求出H、I的坐标以及四边形BHIK周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
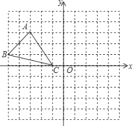
【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
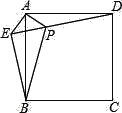
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%, ①这种商品A的进价为多少元?
②现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com