
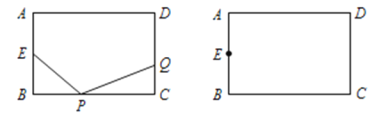
【题目】已知:如图,在长方形![]() 中,AB=4cm,BC=6cm,点
中,AB=4cm,BC=6cm,点![]() 为
为![]() 中点,如果点
中点,如果点![]() 在线段
在线段![]() 上以每秒2cm的速度由点
上以每秒2cm的速度由点![]() 向点
向点![]() 运动,同时,点
运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.设点
运动.设点![]() 运动时间为
运动时间为![]() 秒,若某一时刻△BPE与△CQP全等,求此时
秒,若某一时刻△BPE与△CQP全等,求此时![]() 的值及点
的值及点![]() 的运动速度.
的运动速度.
【答案】见解析
【解析】
由∠B=∠C=90°,可知存在以下两种情况使△BPE≌△CQP,(1)当BP=CP,BE=CQ时;(2)当BP=CQ,BE=CP时;设点Q的运动的时间为vcm/s,则由已知易得BP=2t,CP=6-2t,BE=2,CQ=vt,由此根据上述两种情况分别列出关于t和v的方程,解方程即可求得对应的t和v的值.
设点 ![]() 的运动速度为v cm/s,则
的运动速度为v cm/s,则 ![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵∠B=∠C=90°,
∴存在以下两种情况使△BPE≌△CPQ.
(1)当BP=CP,BE=CQ时,△BPE≌△CPQ,此时有:
![]() ,
,![]() ,
,
解得:![]() ,
,![]() ;
;
(2)当当BP=CQ,BE=CP时,△BPE≌△CPQ,
此时有:![]() ,
,![]() .
.
解得:![]() ,
,![]() .
.
综上所述,![]() 的值为
的值为 ![]() 秒,
秒,![]() 点的速度为
点的速度为![]() ;或
;或![]() 的值为
的值为![]() 秒,
秒,![]() 点的速度为2 cm/s.
点的速度为2 cm/s.


科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
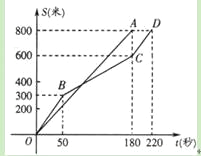
A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
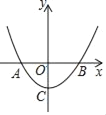
【题目】如图,二次函数y=x2﹣m2(m>0且为常数)的图象与x轴交于点A、B(A在B左侧),与y轴交于C.
(1)求A,B,C三点的坐标(用含m的式子表示);
(2)若∠ACB=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
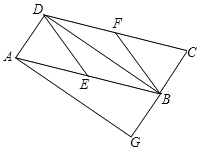
(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
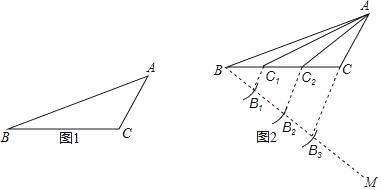
【题目】石景山区八角北路有一块三角形空地(如图1)准备绿化,拟从点A出发,将△ABC分成面积相等的三个三角形,栽种三种不同的花草.
下面是小美的设计(如图2).
作法:(1)作射线BM;
(2)在射线BM上顺次截取BB1=B1B2=B2B3;
(3)连接B3C,分别过B1、B2作B1C1∥B2C2∥B3C,交BC于点C1、C2;
(4)连接AC1、AC2.则![]() .
.
请回答,![]() 成立的理由是:
成立的理由是:
①_____;
②_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
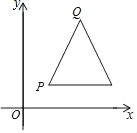
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若PQ为某个等腰三角形的腰,且该等腰三角形的底边与x轴平行,则称该等腰三角形为点P,Q的“相关等腰三角形”.下图为点P,Q的“相关等腰三角形”的示意图.
(1)已知点A的坐标为(0,1),点B的坐标为(-![]() ,0),则点A,B的“相关等腰三角形”的顶角为 °;
,0),则点A,B的“相关等腰三角形”的顶角为 °;
(2)若点C的坐标为(0,![]() ),点D在直线y=4
),点D在直线y=4![]() 上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
(3)⊙O的半径为![]() ,点N在双曲线y=﹣
,点N在双曲线y=﹣![]() 上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(12,0),O为坐标原点,P是线段OA上任一点(不含端点O、A),二次函数y1的图象过P、O两点,二次函数y2的图象过P、A两点,它们的开口均向下,顶点分别为B、C,射线OB与射线AC相交于点D.则当OD=AD=9时,这两个二次函数的最大值之和等于( )
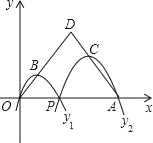
A. 8 B. 3![]() C. 2
C. 2![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
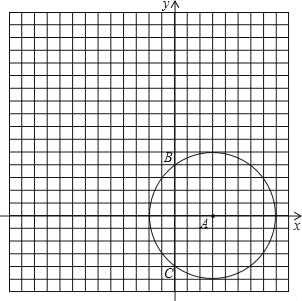
【题目】如图,正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系,圆心为 A(3,0)的⊙A被y轴截得的弦长BC=8.
解答下列问题:
(1)求⊙A 的半径;
(2)请在图中将⊙A 先向上平移 6 个单位,再向左平移8个单位得到⊙D,并写出圆心D的坐标;
(3)观察你所画的图形,对⊙D 与⊙A 的位置关系作出合情的猜想,并直接写出你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com