在平面直角坐标系中,点O是坐标原点,点P(m,-1)(m>0).连接OP,将线段OP绕点O按逆时针方向旋转90°得到线段OM,且点M是抛物线y=ax2+bx+c的顶点.
(1)若m=1,抛物线y=ax2+bx+c经过点(2,2),当0≤x≤1时,求y的取值范围;
(2)已知点A(1,0),若抛物线y=ax2+bx+c与y轴交于点B,直线AB与抛物线y=ax2+bx+c有且只有一个交点,请判断△BOM的形状,并说明理由.
分析:(1)分别过P、M作x、y轴的垂线,设垂足为Q、N;通过证△MON≌△OPQ,可求出MN、ON的长,即可得到M点的坐标;根据M点的坐标,即可求出抛物线的解析式;结合自变量的取值范围及抛物线的对称轴方程即可求得y的取值范围;
(2)在(1)中已经求得M(1,m),可用a、m表示出抛物线的解析式(顶点式),进而可求出B点的坐标;用待定系数法即可得到直线AB的解析式,联立直线AB与抛物线的解析式,由于两个函数只有一个交点,那么所得方程的△=0,由此可求出m、a的关系式,即可用m表示出B点的坐标,然后分别求出△BOM的边长,然后判断△BOM的形状.
解答: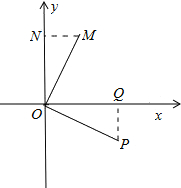
解:(1)∵线段OP绕点O按逆时针方向旋转90°得到线段OM
∴∠POM=90°,OP=OM
过点P(m,-1)作PQ⊥x轴于Q,过点M作MN⊥y轴于N,
∵∠POQ+∠MOQ=90°
∠MON+∠MOQ=90°
∴∠MON=∠POQ
∴∠ONM=∠OQP=90°
∴△MON≌△OPQ
∴MN=PQ=1,ON=OQ=m
∴M(1,m)
∵m=1
∴M(1,1)
∵点M是抛物线y=a(x-1)
2+1
∵抛物线经过点(2,2)
∴a=1
∴y=(x-1)
2+1
∴此抛物线开口向上,对称轴为x=1
∴当x=0时,y=2,
当x=1时,y=1
∴y的取值范围为1≤y≤2.
(2)∵点M(1,m)是抛物线y=ax
2+bx+c的顶点
∴可设抛物线为y=a(x-1)
2+m
∵y=a(x-1)
2+m=ax
2-2ax+a+m
∴B(0,a+m)
又∵A(1,0)
∴直线AB的解析式为y=-(a+m)x+(a+m)
解方程组
| | y=ax2-2ax+a+m | | y=-(a+m)x+(a+m) |
| |
得ax
2+(m-a)x=0
∵直线AB与抛物线y=ax
2+bx+c有且只有一个交点,
∴△=(m-a)
2=0
∴m=a
∴B(0,2m).
在Rt△ONM中,由勾股定理得
OM
2=MN
2+ON
2=1+m
2∴BM=OM
∴△BOM是等腰三角形.
点评:此题考查了图形的旋转变换、全等三角形的判定和性质、函数图象交点坐标的求法以及等腰三角形的判定等知识.

 解:(1)∵线段OP绕点O按逆时针方向旋转90°得到线段OM
解:(1)∵线段OP绕点O按逆时针方向旋转90°得到线段OM

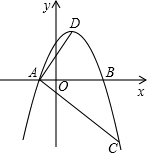 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=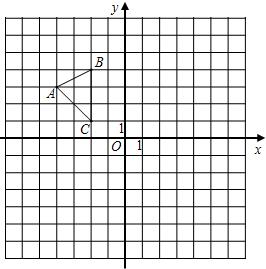 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.