
分析 把$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$化为$\sqrt{(x-0)^{2}+(0-2)^{2}}$+$\sqrt{(3-x)^{2}+(0-4)^{2}}$根据两点间的距离得到$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$的最小值=3$\sqrt{5}$,解方程即可得到结论.
解答 解;求代数式$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$的最小值,即求$\sqrt{{x}^{2}+4}$+$\sqrt{(3-x)^{2}+16}$的最小值,
∴$\sqrt{(x-0)^{2}+(0-2)^{2}}$+$\sqrt{(3-x)^{2}+(0-4)^{2}}$的最小值,
实际上就是求x轴上一点到(0,-2)以及(3,4)两点的和的最小值,
而两点间的距离是线段最短,所以,点到(0,-2)到点(3,4)的距离即为所求,
即$\sqrt{{3}^{2}+(4+2)^{2}}$=3$\sqrt{5}$,
∴$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$的最小值=3$\sqrt{5}$,
解$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$=3$\sqrt{5}$得x=-1,
∴当x为-1时,$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$取得最小值.
点评 本题考查了轴对称-最短路线问题,解方程,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
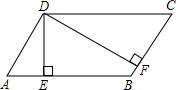 如图,在平行四边形ABCD中,DE⊥AB,DF⊥BC,若DE+DF=10,平行四边形ABCD的边长AB=9,BC=6,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,DE⊥AB,DF⊥BC,若DE+DF=10,平行四边形ABCD的边长AB=9,BC=6,求平行四边形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
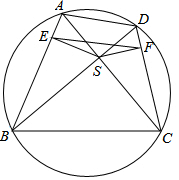 如图所示,圆的内接四边形ABCD的两条对角线AC、BD的交点为S,S在边AB、CD上的投影分别为E、F.证明EF的中垂线平分线段AD、BC.
如图所示,圆的内接四边形ABCD的两条对角线AC、BD的交点为S,S在边AB、CD上的投影分别为E、F.证明EF的中垂线平分线段AD、BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0.5m/s,求这个人走了多长时间?
如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0.5m/s,求这个人走了多长时间?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 大于1.55米且小于1.65米 | B. | 不小于1.55米且小于1.65米 | ||
| C. | 大于1.55米且不大于1.65米 | D. | 不小于1.55米且不大于1.65米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 8 | C. | 2或8 | D. | 8或16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下 | B. | 顶点坐标是(-1,2) | C. | 对称轴是x=1 | D. | 与x轴有两个交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com