练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知点（3，m-1），（m，2）都在一个正比例函数的图象上，求：
    （1）m的值；
    （2）这个正比例函数的解析式．

    分析 设正比例函数解析式为y=kx，把已知两点的坐标代入可得到关于k、m的方程组，可求得m、k的值，则可求得正比例函数解析式．

    解答 解：
    设正比例函数解析式为y=kx，
    把已知点的坐标代入可得$\left\{\begin{array}{l}{3k=m-1}\\{km=2}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-1}\\{m=-2}\end{array}\right.$或$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{m=3}\end{array}\right.$，
    （1）m的值为-2或3；
    （2）正比例函数解析式为y=-x或y=$\frac{2}{3}$x．

    点评 本题主要考查正比例函数解析式的求法，掌握待定系数法的应用步骤是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．（1）如图①，在△ABC中，AB=AC，AC边上的高BD=10cm，求AB边上的高CE的长．
    （2）如图②，在△ABC中，AB=AC，AC边上的高AD=10cm，P为BC边上任一点，PA⊥AB于N，求PM+PN的值．
    （3）如图③，在△ABC中，AB=AC，AC边上的高BD=10cm，P为BC延长线上一点，PM⊥AB于M，PN⊥AC于N，在PM+PN，PM-PN中一个为定值，判断出来并求其值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．用因式分解法解下列方程：
    （1）x2=x；
    （2）9x2-289=0；
    （3）x（x-1）-x+1=0；
    （4）（x-4）2=（5-2x）2；
    （5）x2-6x+5=2（1-x）；
    （6）（2x+1）2-5（2x+1）+6=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

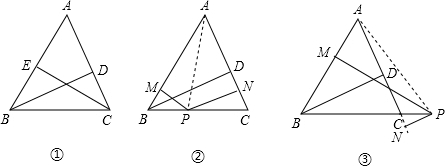
    4．如图，等边△ABC的边长为2，且DB=DC，∠BDC=120°，现有∠MDN=60°，其两边分别与AB，AC交于点M，N，连接MN，将∠MDN绕着D点旋转，使得M，N始终在边AB和边AC上．试判断在这一过程中，△AMN的周长是否发生变化，若没有变化，请求出其周长；若发生变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图所示，属于柱体的一组是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

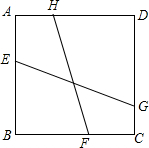    1．如图，正方形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，且EG与FH的夹角为45°，若正方形ABCD的边长为1，FH的长为$\frac{\sqrt{5}}{2}$，求EG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知a，b，c是有理数，满足|a-1|+|b+5|+（5c-1）2=0，求（abc）2012．

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省东莞市堂星晨学校九年级第一次模拟数学试卷（解析版） 题型：填空题

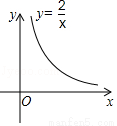
    已知点A（1，y1），B（2，y2）是如图所示的反比例函数y=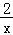图象上两点，则y1__y2（填“＞”，“＜”或“=”）．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷（解析版） 题型：解答题

    如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，过E点作EF∥DC交BC的延长线于点F，连接CD．

    （1）求证：四边形CDEF是平行四边形；

    （2）求EF的长．

    查看答案和解析>>

    同步练习册答案