
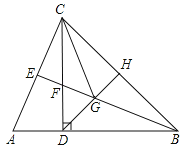
【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG.
(1)求证:△ADC≌△FDB;
(2)求证:CE=![]() BF;
BF;
(3)判断△ECG的形状,并证明你的结论;
(4)猜想BG与CE的数量关系,并证明你的结论.
【答案】(1)证明见解析;(2)证明见解析;(3)△ECG为等腰直角三角形;(4)GB=![]() CE.
CE.
【解析】
试题分析:(1)首先根据AB=BC,BE平分∠ABC,得到BE⊥AC,CE=AE,进一步得到∠ACD=∠DBF,结合CD=BD,即可证明出△ADC≌△FDB;
(2)由△ADC≌△FDB得到AC=BF,结合CE=AE,即可证明出结论;
(3)由点H是BC边的中点,得到GH垂直平分BC,即GC=GB,由∠DBF=∠GBC=∠GCB=∠ECF,得∠ECO=45°,结合BE⊥AC,即可判断出△ECG的形状;
(4)由△ECG为等腰直角三角形,得到GC=![]() CE,因为GC=GB,即可得到GB=
CE,因为GC=GB,即可得到GB=![]() CE.
CE.
试题解析:(1)∵AB=BC,BE平分∠ABC,∴BE⊥AC,CE=AE,∵CD⊥AB,∴∠ACD=∠DBF,在△ADC和△FDB中,∵∠ACD=∠DFB,CD=BD,∠ADC=∠BDF,∴△ADC≌△FDB(ASA);
(2)∵△ADC≌△FDB,∴AC=BF,又∵CE=AE,∴CE=![]() BF;
BF;
(3)△ECG为等腰直角三角形.∵点H是BC边的中点,∴GH垂直平分BC,∴GC=GB,∵∠DBF=∠GBC=∠GCB=∠ECF,得∠ECG=45°,又∵BE⊥AC,∴△ECG为等腰直角三角形;
(4)GB=![]() CE;
CE;
∵△ECG为等腰直角三角形,∴GC=![]() CE,∵GC=GB,∴GB=
CE,∵GC=GB,∴GB=![]() CE.
CE.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+a,下列说法中正确的是 (填写序号).
①当x<0时,y随x的增大而减小;
②若图象与x轴有交点,则a≤4;
③若将图象向上平移1个单位长度,再向左平移3个单位长度后过点(1,﹣2),则a=﹣3;
④当a=3时,不等式x2﹣4x+a>0的解集是1<x<3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图:
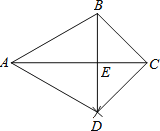
①以A为圆心,AB长为半径画弧;
②以C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD,CD.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区截止到今年栽有果树2400棵,计划今后每年栽果树300棵,x年后,总共栽有果树y棵,则y与x之间的关系式为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把形状、大小、质地完全相同的4张卡片分别标上数字﹣1、﹣4、0、2,将这4张卡片放入不透明的盒子中搅匀.求下列事件的概率:
(1)从中随机抽取一张卡片,卡片上的数字是负数;
(2)先从盒子中随机抽取一张卡片不放回,再随机抽取一张,两张卡片上的数字之积为0(用列表法或树形图).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com