
【题目】已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.

【答案】(1)见解析;(2) EF⊥AE仍成立,理由见解析.
【解析】
(1)如图1,先根据三角形内角和定理得出∠BAE=180°-∠B-∠AEB,∠EFC=180°-∠C-∠CEF,由∠B=∠C,∠AEB=∠CEF,得到∠BAE=∠EFC,再由角平分线定义得出∠BAE=∠DAE,等量代换得到∠EFC=∠DAE.由平角的定义得出∠EFC+∠EFD=180°,那么∠DAE+∠EFD=180°,再根据四边形内角和定理求出∠AEF+∠D=360°-(∠DAE+∠EFD)=180°,进而得到∠AEF=90°,由垂直的定义证明出EF⊥AE;
(2)如图2,先根据三角形外角的性质得出∠1=∠ABC-∠AEB,∠F=∠BCD-∠CEF,由∠ABC=∠BCD,∠AEB=∠CEF,得到∠1=∠F,再由角平分线定义得出∠1=∠2,等量代换得到∠F=∠2.由平角的定义得出∠2+∠EAD=180°,那么∠F+∠EAD=180°,再根据四边形内角和定理求出∠AEF+∠D=360°-(∠F+∠EAD)=180°,进而得到∠AEF=90°,由垂直的定义得出EF⊥AE.
(1)证明:如图1,∵∠BAE=180°-∠B-∠AEB,∠EFC=180°-∠C-∠CEF,
∠B=∠C,∠AEB=∠CEF,
∴∠BAE=∠EFC,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠EFC=∠DAE.
∵∠EFC+∠EFD=180°,
∴∠DAE+∠EFD=180°,
∴∠AEF+∠D=360°-(∠DAE+∠EFD)=180°,
∵∠D=90°,
∴∠AEF=90°,
∴EF⊥AE;
(2)解:如图2,若AE平分∠BAD的外角,其余条件不变,(1)中结论没有变化.理由如下:
∵∠1=∠ABC-∠AEB,∠F=∠BCD-∠CEF,
∠ABC=∠BCD,∠AEB=∠CEF,
∴∠1=∠F,
∵AE平分∠BAD的外角,
∴∠1=∠2,
∴∠F=∠2.
∵∠2+∠EAD=180°,
∴∠F+∠EAD=180°,
∴∠AEF+∠D=360°-(∠F+∠EAD)=180°,
∵∠D=90°,
∴∠AEF=90°,
∴EF⊥AE.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E,F.
(1)若CE=4,CF=3,求OC的长.
(2)连接AE、AF,问当点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
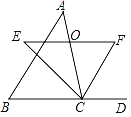
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习一元一次方程的解法时,我们经常遇到这样的试题:
“解方程:![]() ”,请根据解题过程,在后面的括号内写出变形依据.
”,请根据解题过程,在后面的括号内写出变形依据.
解:去分母,得 ( )
去括号,得 ( )
移项,得 ( )
合并,得 (合并同类项法则)
系数化为 1,得 ( )
请你写出在进行运算时容易出错的地方(至少写出三个).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校有一个长方形广场,在广场的中央设计一个圆形花坛,四角都设计四分之一圆形的花坛.若长方形的长为am,宽为bm,中央圆形的半径和四个四分之一圆形的半径都为rm.
(1)列式表示广场空地的面积;(不写过程,直接写出答案)
(2)学校准备在广场四周种树,七年级四个班的学生在植树节当天进行义务植树,一班植树 x棵,二班植树的棵数比一班的多10棵,三班植树的棵数比二班的2倍少30棵,四班植树的棵数比三班的一半多20棵,求四个班一共植树多少棵?(用含x的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机器零件的横截面如图所示,按要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°,∠D=31°,∠AED=143°,请你帮他判断该零件是否合格:___.(填“合格”或“不合格”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣(a+1)x﹣3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
(1)求抛物线的表达式;
(2)当m=2时,△PQR为等腰直角三角形,求点P的坐标;
(3)①求PR+QR的最大值;②求△PQR面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( )
(x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( ) 
A.2
B.4
C.2 ![]()
D.4 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com