
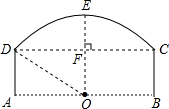
 如图为桥洞的形状,其正视图是由$\widehat{CD}$和矩形ABCD构成.O点为$\widehat{CD}$所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求$\widehat{CD}$所在⊙O的半径DO.
如图为桥洞的形状,其正视图是由$\widehat{CD}$和矩形ABCD构成.O点为$\widehat{CD}$所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求$\widehat{CD}$所在⊙O的半径DO. 科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:单选题
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件是( )

A. AC⊥BD B. AC=BD C. AC⊥BD且AC=BD D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
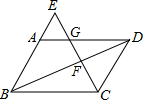 如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$.
如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com