【题目】作图：
（1）如图甲，以点O为中心，把点P顺时针旋转45°；
（2）如图乙，以点O为中心，把线段AB逆时针旋转90°；
（3）如图丙，以点O为中心，把△ABC顺时针旋转120°；
（4）如图丁，以点B为中心，把△ABC旋转180°．
【答案】（1）作图见解析；（2）作图见解析；（3）作图见解析；（4）作图见解析.
【解析】试题分析:(1)连接OP,将OP顺时针旋转45°,即可得到P的对应点P′,
(2)根据旋转角为90°,旋转方向是逆时针,旋转中心为O可找出旋转后各点的对应点,然后顺次连接即可,
(3)根据旋转角为120°,旋转方向是顺时针,旋转中心为O可找出旋转后各点的对应点,然后顺次连接即可,
(4) 根据旋转角为180°,旋转中心为B可找出旋转后各点的对应点,然后顺次连接即可.
试题解析:
（1）如图甲,点P′为所求,
（2）如图乙,线段A′B′为所求,
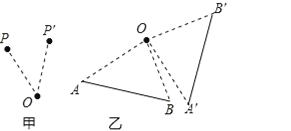
（3）如图丙,△A′B′C′为所求,
（4）如图丁,△A′BC′为所求.
科目：初中数学 来源： 题型：
【题目】如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（ ）
A. ∠1＝∠2＋∠A B. ∠1＝2∠A＋∠2
C. ∠1＝2∠2＋2∠A D. 2∠1＝∠2＋∠A
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】利用勾股定理可以在数轴上画出表示
的点，请依据以下思路完成画图，并保留画图痕迹：
第一步：（计算）尝试满足
，使其中a，b都为正整数.你取的正整数a=____，b=________；
第二步：（画长为
的线段）以第一步中你所取的正整数a，b为两条直角边长画Rt△OEF，使O为原点，点E落在数轴的正半轴上， 
，则斜边OF的长即为
.
请在下面的数轴上画图：（第二步不要求尺规作图，不要求写画法）
第三步：（画表示
的点）在下面的数轴上画出表示
的点M，并描述第三步的画图步骤：_______________________________________________________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】实验与探究：
（
）如图，直线
为第一、三象限的角平分线，观察易知
关于直线
的对称点
的坐标为
，请在图中分别标明
、
关于直线
的对称点
、
的位置，并写出他们的坐标： 
__________、
__________．
（
）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点
关于第一、三象限的角平分线
的对称点
的坐标为__________ (不必证明)．
（
）已知两点
、
，在直线
上是否存在一点
，使点
到
、
两点的距离之和最小，并求出最小距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC＝120°．以D为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在△ABC中，点D在边AC上，下列条件中，能判断△BDC与△ABC相似的是 ( )
A. AB·CB=CA·CD B. AB·CD=BD·BC C. BC2=AC·DC D. BD2=CD·DA
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：
（1）①若∠DCE=45°，则∠ACB的度数为 ；
②若∠ACB=140°，求∠DCE的度数；
（2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．
（3）当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由）；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，E、B、F、C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（ ）
A. AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
