
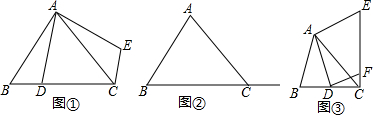
分析 (1)线段AD绕点A逆时针旋转90°得到AE,根据旋转的性质得到AD=AE,∠BAD=∠CAE,得到△BAD≌△CAE,CE=BD,∠ACE=∠B,得到∠BCE=∠BCA+∠ACE=90°,于是有CE=BD,CE⊥BD.
(2)证明的方法与(1)一样.
(3)过A作AM⊥BC于M,EN⊥AM于N,根据旋转的性质得到∠DAE=90°,AD=AE,利用等角的余角相等得到∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA,则NE=MA,由于∠ACB=45°,则AM=MC,所以MC=NE,易得四边形MCEN为矩形,得到∠DCF=90°,
由此得到Rt△AMD∽Rt△DCF,得$\frac{MD}{CF}=\frac{AM}{DC}$,设DC=x,而∠ACB=45°,AC=$\sqrt{2}$,得AM=CM=3,MD=3-x,利用相似比可得到CF=-$\frac{1}{3}$x2+1,再利用二次函数即可求得CF的最大值.
解答 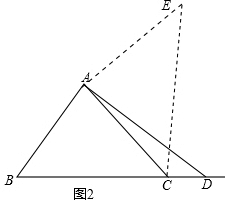 解:(1)①∵AB=AC,∠BAC=90°,
解:(1)①∵AB=AC,∠BAC=90°,
∴线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠BAD=∠CAE,
∴△BAD≌△CAE,
∴CE=BD,∠ACE=∠B,
∴∠BCE=∠BCA+∠ACE=90°,
∴线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
故答案为:CE=BD,CE⊥BD;
(2)(1)中的结论仍然成立.理由如下:
如图2,
∵线段AD绕点A逆时针旋转90°得到AE,
∴AE=AD,∠DAE=90°,
∵AB=AC,∠BAC=90°
∴∠CAE=∠BAD,
∴△ACE≌△ABD,
∴CE=BD,∠ACE=∠B,
∴∠BCE=90°,
所以线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
(3)45°;$\frac{3}{4}$;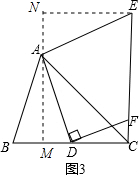
过A作AM⊥BC于M,过E点作EN垂直于MA延长线于N,如图3,
∵线段AD绕点A逆时针旋转90°得到AE,
∴∠DAE=90°,AD=AE,
∴∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA,
∴NE=AM,
∵CE⊥BD,即CE⊥MC,∴∠NEC=90°,
∴四边形MCEN为矩形,
∴NE=MC,∴AM=MC,
∴∠ACB=45°,
∵四边形MCEN为矩形,
∴Rt△AMD∽Rt△DCF,
∴$\frac{MD}{CF}$=$\frac{AM}{DC}$,设DC=x,
∵在Rt△AMC中,∠ACB=45°,AC=3$\sqrt{2}$,
∴AM=CM=3,MD=3-x,∴$\frac{3-x}{CF}$=$\frac{3}{x}$,
∴CF=-$\frac{1}{3}$x2+x=-$\frac{1}{3}$(x-$\frac{3}{2}$)2+$\frac{3}{4}$,
∴当x=$\frac{3}{2}$时有最大值,最大值为$\frac{3}{4}$.
故答案为:45°,$\frac{3}{4}$.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等腰直角三角形的性质和三角形全等及相似的判定与性质.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
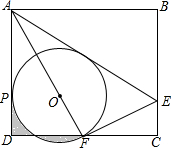 如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3$\sqrt{3}$,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=$\frac{9}{2}$CE;④S阴影=$\frac{{\sqrt{3}}}{2}$.其中正确结论的序号是①②④.
如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3$\sqrt{3}$,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=$\frac{9}{2}$CE;④S阴影=$\frac{{\sqrt{3}}}{2}$.其中正确结论的序号是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4×108 | B. | 4×10-8 | C. | 0.4×108 | D. | -4×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
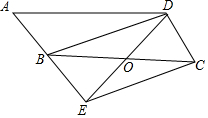 如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com