
【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:(1)EH=FH;
(2)∠CAB=2∠CDH.

【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)根据余角的性质得到∠AFD=∠AEC,证得∠CFE=∠CEF,得到CF=CE,根据等腰三角形的性质即可得到结论.
(2)由于∠ADF=∠CHF=90°,∠AFD=∠CFH,得到△ADF∽△CFH,根据相似三角形的性质得到![]() ,由于∠AFC=∠DFH,得到△AFC∽△DFH,根据相似三角形的性质得到∠CAF=∠CDH,等量代换即可得到结论.
,由于∠AFC=∠DFH,得到△AFC∽△DFH,根据相似三角形的性质得到∠CAF=∠CDH,等量代换即可得到结论.
试题解析:
(1)证明:∵∠ACB=90°,CD⊥AB于D,
∴∠CAE+∠AEC=∠DAF+∠AFD=90°,
∵AE平分∠CAB,
∴∠CAE=∠DAF,
∴∠AFD=∠AEC,
∵∠AFD=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE,
∵CH⊥EF,
∴HE=HF;
(2)证明:∵∠ADF=∠CHF=90°,∠AFD=∠CFH,
∴△ADF∽△CFH,
∴![]() ,
,
∵∠AFC=∠DFH,
∴△AFC∽△DFH,
∴∠CAF=∠CDH,
∵∠CAD=2∠CAF,
∴∠CAB=2∠CDH.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() .
.
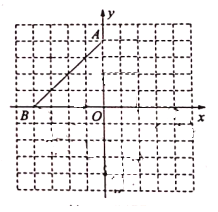
(1)①画出线段![]() 关于
关于![]() 轴对称的线段
轴对称的线段![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;
②将线段![]() 平移至
平移至![]() ,其中点
,其中点![]() 与点
与点![]() 对应,画出线段
对应,画出线段![]() 并写出点
并写出点![]() 的坐标;
的坐标;
(2)点![]() 在(1)中四边形
在(1)中四边形![]() 边
边![]() 上,且
上,且![]() 是对角线
是对角线![]() 上--动点,则
上--动点,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中∠ONM=30![]() ,∠OCD=45
,∠OCD=45![]()
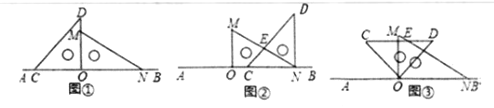
(1)观察猜想
将图1中的三角尺OCD沿AB的方向平移至图②的位置,使得点O与点N重合,CD与MN相交于点E,则∠CEN= ![]() .
.
(2)操作探究
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在∠MON的内部,如图3,且OD恰好平分∠MON,CD与NM相交于点E,求∠CEN的度数;
(3)深化拓展
将图1中的三角尺OCD绕点O按沿顺时针方向旋转一周,在旋转的过程中,当边OC旋转 ![]() 时,边CD恰好与边MN平行。(直接写出结果)
时,边CD恰好与边MN平行。(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )

A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费.假设这两位家长带领x名学生去旅行,甲、乙旅行社的收费分别为y甲,y乙,
(1)写出y甲,y乙与x的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过
,过![]() 的中点
的中点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() .
.

(1)求![]() ,
,![]() 两点的坐标及直线
两点的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)若坐标平面内的点![]() ,能使以点
,能使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形,请直接写出满足条件的点
为顶点的四边形为平行四边形,请直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
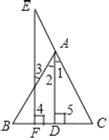
【题目】已知,如图所示,AD⊥BC于D,EF⊥BC于F,∠3=∠E,说明AD是∠BAC的角平分线请你完成下列说理过程(在横线上填上适当的内容,在括号内写出说理依据).
理由:∵AD⊥BC,EF⊥BC(已知)
∴∠4=∠5=90°( ),
∴AD∥EF( ),
∴∠1= ( ),
∠2= ( ),
又∵∠E=∠3(已知)
∴ ( ),
即AD是∠BAC的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
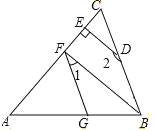
【题目】如图所示,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系?并说明理由;
(2)如果,DE⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com