
【题目】已知,抛物线的顶点坐标为(2,1),与y轴交于点(0,3).求
(1)这条抛物线的表达式;
(2)直接写出当1<x<5时,y的取值范围为 .
【答案】(1)抛物线的解析式为:y=![]() (x﹣2)2+1;(2)1≤y<
(x﹣2)2+1;(2)1≤y<![]() .
.
【解析】
(1)根据已知抛物线的顶点坐标,则设抛物线的顶点式为y=a(x-2)2+1(a≠0),再把(0,3)代入可计算出a的值即可,
(2)求得抛物线的最小值,然后再求得当x=1和x=5时的函数值,即可求得当1<x<5时,y的取值.
解:(1)∵抛物线的顶点坐标为(2,1)
∴设抛物线的解析式为y=a(x﹣2)2+1(a≠0),
把(0,3)代入得:4a+1=3,
解得,a=![]() .
.
所以,这条抛物线的解析式为:y=![]() (x﹣2)2+1;
(x﹣2)2+1;
(2)由y=![]() (x﹣2)2+1可知,抛物线开口向上,当x=2时,y有最小值1,
(x﹣2)2+1可知,抛物线开口向上,当x=2时,y有最小值1,
当x=1时,y=![]() ;当x=5时,y=
;当x=5时,y=![]() ,
,
∴当1<x<5时,y的取值范围为1≤y<![]() ,
,
故答案为1≤y<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN重合,其量角器最外缘的读数是从N点开始(即N点的读数为0),现有射线CP绕着点C从CA顺时针以每秒2度的速度旋转到与△ACB外接圆相切为止.在旋转过程中,射线CP与量角器的半圆弧交于E.
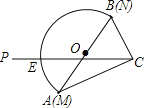
(1)当射线CP与△ABC的外接圆相切时,求射线CP旋转度数是多少?
(2)当射线CP分别经过△ABC的外心、内心时,点E处的读数分别是多少?
(3)当旋转7.5秒时,连接BE,求证:BE=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司规定:一名客户如果一个月的通话时间不超过![]() 分钟,那么这个月这名客户只要交10元通话费;如果超过
分钟,那么这个月这名客户只要交10元通话费;如果超过![]() 分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟
分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟![]() 元交费.
元交费.
(Ⅰ)某名客户7月份通话90分钟,超过了规定的![]() 分钟,则超过部分应交通话费______元(用含
分钟,则超过部分应交通话费______元(用含![]() 的代数式表示);
的代数式表示);
(Ⅱ)下表表示某名客户8月份、9月份的通话情况和交费情况:
月份 | 通话时间/分钟 | 通话费总数/元 |
8月份 | 80 | 25 |
9月份 | 45 | 10 |
根据上表的数据,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图1.已知∠ACB=∠ADB=90°,请用尺规作图作出△ABD的外接圆(保留作图痕迹,不写作法);点C是否在△ABD的外接圆上 (填“是”或“否”).
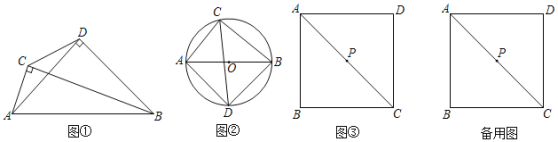
问题探究
(2)如图2.四边形ADBC是⊙O的内接四边形,∠ACB=∠ADB=90°,AD=BD.求证:CA+CB=![]() CD;
CD;
(3)如图3.点P是正方形ABCD对角线AC的中点,点E是平面上一点,EB=AB且EA=![]() BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:
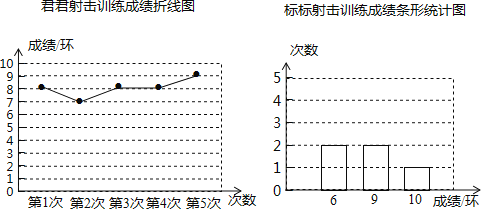
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A′在Rt△ABC的边AB上,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,A'B'与BC交于点D,连接BB′,求线段BB′的长度.
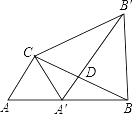
查看答案和解析>>
科目:初中数学 来源: 题型:
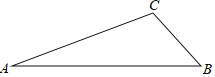
【题目】如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com