
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
【答案】
(1)证明:∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,
∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,
∴∠BAC+∠3=∠EAF+∠3,即∠BAE=∠CAF,
在△ABE和△ACF中
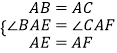 ,
,
∴△ABE≌△ACF,
∴BE=CF;

(2)解:∵四边形ABDF为菱形,
∴DF=AF=2,DF∥AB,
∴∠1=∠BAC=45°,
∴△ACF为等腰直角三角形,
∴CF= ![]() AF=2
AF=2 ![]() ,
,
∴CD=CF﹣DF=2 ![]() ﹣2.
﹣2.
【解析】(1)根据旋转的性质得AE=AF=AB=AC=2,∠EAF=∠BAC=45°,然后根据“SAS”证明△ABE≌△ACF,于是根据全等三角形的性质即可得到结论;(2)根据菱形的性质得DF=AF=2,DF∥AB,再利用平行线的性质得∠1=∠BAC=45°,则可判断△ACF为等腰直角三角形,所以CF= ![]() AF=2
AF=2 ![]() ,然后计算CF﹣DF即可.
,然后计算CF﹣DF即可.


科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.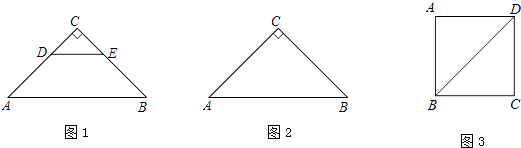
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为 ![]() ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | ﹣4 | ﹣4 | 0 | 8 |
(1)根据上表填空; ①方程ax2+bx+c=0的两个根分别是和 .
②抛物线经过点(﹣3,);
③在对称轴左侧,y随x增大而;
(2)求抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安徽某中学组织学生举行“创建文明城市”宣传活动,从学校坐车出发,先上坡到达![]() 地后,宣传8分钟;然后下坡到
地后,宣传8分钟;然后下坡到![]() 地宣传8分钟返回,行程情况如图。若返回时,上、下坡速度仍保持不变,在
地宣传8分钟返回,行程情况如图。若返回时,上、下坡速度仍保持不变,在![]() 地仍要宣传8分钟,那么他们从
地仍要宣传8分钟,那么他们从![]() 地返回学校用的时间是 _____
地返回学校用的时间是 _____
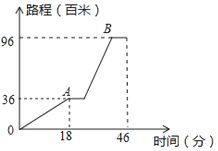
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a﹣b+c>0,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣ ![]() ,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号)
,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,1),B(-2,0),以坐标原点O为位似中心,将线段AB放大2倍,放大后的线段A′B′与线段AB在同一侧,则两个端点A′,B′的坐标分别为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com