
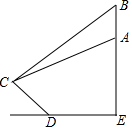
 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)| A. | 91.1 | B. | 91.3 | C. | 58.2 | D. | 58.4 |
分析 作CP⊥BE、CQ⊥DE,设AP=x,知CP=$\sqrt{3}$x,根据BP=CP建立方程求出x的值,即可得CP=QE=100$\sqrt{3}$+300,QD=CP-DE=100$\sqrt{3}$-100,由$\frac{CQ}{QD}$=$\frac{3}{4}$知$\frac{QD}{CD}$=$\frac{4}{5}$,从而得CD=$\frac{5}{4}$QD,即可得出答案.
解答 解:如图,作CP⊥BE于点P,作CQ⊥DE于点Q,
由题意知∠ACP=30°,∠BCP=45°,
设AP=x,则CP=$\frac{AP}{tan∠ACP}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,
∵∠BCP=45°,
∴BP=CP,即$\sqrt{3}$x=200+x,
解得:x=100+100$\sqrt{3}$,
∴CP=$\sqrt{3}$x=100$\sqrt{3}$+300,
∵DE=400,
∴QD=QE-DE=CP-DE=100$\sqrt{3}$+300-400=100$\sqrt{3}$-100,
∵$\frac{CQ}{QD}$=$\frac{3}{4}$,
∴$\frac{QD}{CD}$=$\frac{4}{5}$,
则CD=$\frac{5}{4}$QD=$\frac{5}{4}$(100$\sqrt{3}$-100)≈91.3(米),
故选:B.
点评 本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1.
如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com