
”¾ĢāÄæ”æĪŅĆĒøų³öČēĻĀ¶ØŅå£ŗĖ³“ĪĮ¬½ÓČĪŅāŅ»øöĖıߊĪø÷±ßÖŠµćĖłµĆµÄĖıߊĪ½ŠÖŠµćĖıߊĪ£®
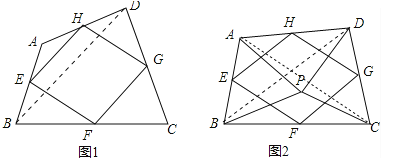
£Ø1£©ČēĶ¼1£¬ĖıߊĪABCDÖŠ£¬µćE£¬F£¬G£¬H·Ö±šĪŖ±ßAB£¬BC£¬CD£¬DAµÄÖŠµć£®
ĒóÖ¤£ŗÖŠµćĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČēĶ¼2£¬µćPŹĒĖıߊĪABCDÄŚŅ»µć£¬ĒŅĀś×ćPA=PB£¬PC=PD£¬”ĻAPB=”ĻCPD£¬µćE£¬F£¬G£¬H·Ö±šĪŖ±ßAB£¬BC£¬CD£¬DAµÄÖŠµć£¬²ĀĻėÖŠµćĖıߊĪEFGHµÄŠĪד£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£»
£Ø3£©Čōøıä£Ø2£©ÖŠµÄĢõ¼ž£¬Ź¹”ĻAPB=”ĻCPD=90”ć£¬ĘäĖūĢõ¼ž²»±ä£¬Ö±½ÓŠ“³öÖŠµćĖıߊĪEFGHµÄŠĪד£®£Ø²»±ŲÖ¤Ć÷£©

”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£»£Ø2£©ĖıߊĪEFGHŹĒĮāŠĪ£»£Ø3£©ĖıߊĪEFGHŹĒÕż·½ŠĪ£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬Į¬½ÓBD£¬øł¾ŻČż½ĒŠĪÖŠĪ»Ļß¶ØĄķÖ»ŅŖÖ¤Ć÷EH”ĪFG£¬EH=FG¼“æÉ£®
£Ø2£©ĖıߊĪEFGHŹĒĮāŠĪ£®ĻČÖ¤Ć÷”÷APC”Õ”÷BPD£¬µĆµ½AC=BD£¬ŌŁÖ¤Ć÷EF=FG¼“æÉ£®
£Ø3£©ĖıߊĪEFGHŹĒÕż·½ŠĪ£¬Ö»ŅŖÖ¤Ć÷”ĻEHG=90”ć£¬ĄūÓĆ”÷APC”Õ”÷BPD£¬µĆ”ĻACP=”ĻBDP£¬¼“æÉÖ¤Ć÷”ĻCOD=”ĻCPD=90”ć£¬ŌŁøł¾ŻĘ½ŠŠĻߵĊŌÖŹ¼“æÉÖ¤Ć÷£®
ŹŌĢā½āĪö£ŗ£Ø1£©Ö¤Ć÷£ŗČēĶ¼1ÖŠ£¬Į¬½ÓBD£®
”ßµćE£¬H·Ö±šĪŖ±ßAB£¬DAµÄÖŠµć£¬”ąEH”ĪBD£¬EH=![]() BD£¬”ßµćF£¬G·Ö±šĪŖ±ßBC£¬CDµÄÖŠµć£¬”ąFG”ĪBD£¬FG=
BD£¬”ßµćF£¬G·Ö±šĪŖ±ßBC£¬CDµÄÖŠµć£¬”ąFG”ĪBD£¬FG=![]() BD£¬”ąEH”ĪFG£¬EH=GF£¬”ąÖŠµćĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£®
BD£¬”ąEH”ĪFG£¬EH=GF£¬”ąÖŠµćĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£®
£Ø2£©ĖıߊĪEFGHŹĒĮāŠĪ£®
Ö¤Ć÷£ŗČēĶ¼2ÖŠ£¬Į¬½ÓAC£¬BD£®
”ß”ĻAPB=”ĻCPD£¬”ą”ĻAPB+”ĻAPD=”ĻCPD+”ĻAPD£¬¼“”ĻAPC=”ĻBPD£¬ŌŚ”÷APCŗĶ”÷BPDÖŠ£¬”ßAP=PB£¬”ĻAPC=”ĻBPD£¬PC=PD£¬”ą”÷APC”Õ”÷BPD£¬”ąAC=BD£®”ßµćE£¬F£¬G·Ö±šĪŖ±ßAB£¬BC£¬CDµÄÖŠµć£¬”ąEF=![]() AC£¬FG=
AC£¬FG=![]() BD£¬”ßĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£¬”ąĖıߊĪEFGHŹĒĮāŠĪ£®
BD£¬”ßĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£¬”ąĖıߊĪEFGHŹĒĮāŠĪ£®
£Ø3£©ĖıߊĪEFGHŹĒÕż·½ŠĪ£®
Ö¤Ć÷£ŗČēĶ¼2ÖŠ£¬ÉčACÓėBD½»ÓŚµćO£®ACÓėPD½»ÓŚµćM£¬ACÓėEH½»ÓŚµćN£®
”ß”÷APC”Õ”÷BPD£¬”ą”ĻACP=”ĻBDP£¬”ß”ĻDMO=”ĻCMP£¬”ą”ĻCOD=”ĻCPD=90”ć£¬”ßEH”ĪBD£¬AC”ĪHG£¬”ą”ĻEHG=”ĻENO=”ĻBOC=”ĻDOC=90”ć£¬”ßĖıߊĪEFGHŹĒĮāŠĪ£¬”ąĖıߊĪEFGHŹĒÕż·½ŠĪ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōµ„ĻīŹ½2x3y2mÓė©3xny2µÄ²īČŌŹĒµ„ĻīŹ½£¬Ōņm+nµÄÖµŹĒ£Ø””””£©
A. 2 B. 3 C. 4 D. 5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö¶ą±ßŠĪÄŚ½ĒŗĶĶā½ĒŗĶĪŖ1980”ć£¬ŌņĖüŹĒ£Ø £©±ßŠŠ£®
A.Ź®B.Ź®Ņ»C.Ź®¶žD.²»Č·¶Ø
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ5øöŗģĒņ”¢4øö°×Ēņ·ÅČėŅ»øö²»ĶøĆ÷µÄŗŠ×ÓĄļ£¬“ÓÖŠĆž³ö6øöĒņ£¬Ē”ŗĆŗģĒņÓė°×Ēņ¶¼Ćžµ½£¬ÕāøöŹĀ¼ž(””””)
A. ²»æÉÄÜ·¢ÉśB. æÉÄÜ·¢ÉśC. ŗÜæÉÄÜ·¢ÉśD. ±ŲČ»·¢Éś
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
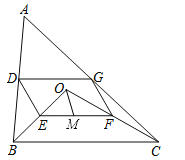
”¾ĢāÄæ”æČēĶ¼£¬µćOŹĒ”÷ABCÄŚŅ»µć£¬Į¬½įOB”¢OC£¬²¢½«AB”¢OB”¢OC”¢ACµÄÖŠµćD”¢E”¢F”¢GŅĄ“ĪĮ¬½į£¬µĆµ½ĖıߊĪDEFG£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪDEFGŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČōMĪŖEFµÄÖŠµć£¬OM=3£¬”ĻOBCŗĶ”ĻOCB»„Óą£¬ĒóDGµÄ³¤¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻß,²¢½«ĖıߊĪ·Ö³É¶ŌČ«µČČż½ĒŠĪ, øöĆ껿ĻąµČµÄČż½ĒŠĪ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»¶ÆµćP“ÓŹżÖįÉĻµÄŌµć³ö·¢£¬°“ĻĀĮŠ¹ęŌņŌĖ¶Æ£ŗ
£Ø1£©ŃŲŹżÖįµÄÕż·½ĻņĻČĒ°½ų5øöµ„Ī»£¬Č»ŗóŗóĶĖ3øöµ„Ī»£¬Čē“Ė·“ø“½ųŠŠ£»
£Ø2£©ŅŃÖŖµćPĆæĆėÖ»ÄÜĒ°½ų»ņŗóĶĖ1øöµ„Ī»£®ÉčXn±ķŹ¾µŚnĆėµćPŌŚŹżÖįÉĻµÄĪ»ÖĆĖł¶ŌÓ¦µÄŹż£¬ŌņX2018ĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com