
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当点P运动到CD上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.
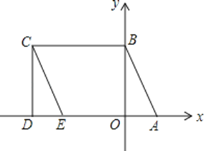
【答案】(1)(-2,0);(2)①t=2;②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);③能确定,z=x+y.
【解析】
(1)根据平移的性质即可得到结论;
(2)①由点C的坐标为(-3,2).得到BC=3,CD=2,由于点P的横坐标与纵坐标互为相反数;于是确定点P在线段BC上,有PB=CD,即可得到结果;
②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);
③如图,过P作PF∥BC交AB于F,则PF∥AD,根据平行线的性质即可得到结论.
解:(1)根据题意,可得
三角形OAB沿x轴负方向平移3个单位得到三角形DEC,
∵点A的坐标是(1,0),
∴点E的坐标是(-2,0);
故答案为:(-2,0);
(2)①∵点C的坐标为(-3,2)
∴BC=3,CD=2,
∵点P的横坐标与纵坐标互为相反数;
∴点P在线段BC上,
∴PB=CD,
即t=2;
∴当t=2秒时,点P的横坐标与纵坐标互为相反数;
故答案为:2;
②当点P在线段BC上时,点P的坐标(-t,2),
当点P在线段CD上时,点P的坐标(-3,5-t);
③能确定,
如图,过P作PF∥BC交AB于F,
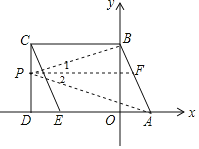
则PF∥AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.


科目:初中数学 来源: 题型:
【题目】小梅将边长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …长的若干个正方形按一定规律拼成不同的长方形,如图所示.
…长的若干个正方形按一定规律拼成不同的长方形,如图所示.
![]() 求第四个长方形的周长;
求第四个长方形的周长;
![]() 当
当![]() 时,求第五个长方形的面积.(用科学记数法表示)
时,求第五个长方形的面积.(用科学记数法表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
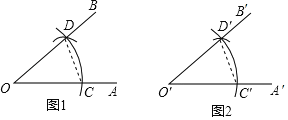
【题目】已知:∠AOB.
求作:∠A'O'B',使∠A'O′B'=∠AOB
(1)如图1,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
(2)如图2,画一条射线O′A′,以点O′为圆心,OC长为半径间弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所而的弧交于点D′;
(4)过点D′画射线O′B',则∠A'O'B'=∠AOB.
根据以上作图步骤,请你证明∠A'O'B′=∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
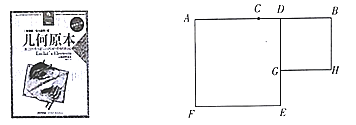
【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点(
上任意一点(![]() 不与
不与![]() 重合),分别以
重合),分别以![]() 和
和![]() 为边在
为边在![]() 的下方作正方形
的下方作正方形![]() 和正方形
和正方形![]() ,以
,以![]() 和
和![]() 为边在线段下方作正方形
为边在线段下方作正方形![]() 和正方形
和正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 的面积之和等于正方形
的面积之和等于正方形![]() 和正方形
和正方形![]() 面积之和的两倍.
面积之和的两倍.
(1)请你画出正方形![]() 和正方形
和正方形![]() (不必尺规作图);
(不必尺规作图);
(2)设![]() ,
,![]() ,根据题意写出关于
,根据题意写出关于![]() 的等式并证明.
的等式并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
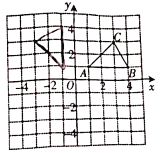
(1)将入![]() 向下平移
向下平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
(2)将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,请画出
,请画出![]() ;
;
(3)判断以![]() 、
、![]() 、
、![]() 为顶点的三角形的形状.(无须说明理由)
为顶点的三角形的形状.(无须说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:
第1个式子: ![]()
第2个式子: ![]()
第3个式子: ![]()
第4个式子: ![]()
![]()
(1)可猜想第7个等式为 .
(2)探索规律,若字母![]() 表示自然数,请写出第
表示自然数,请写出第![]() 个等式 .
个等式 .
(3)试证明你写出的等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+bx+c的图象经过A(0,3),B(﹣4,﹣
x2+bx+c的图象经过A(0,3),B(﹣4,﹣![]() )两点.
)两点.
(1)求b,c的值.
(2)二次函数y=﹣![]() x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
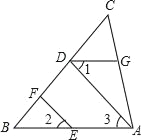
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
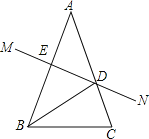
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AC于点D,交AB于E.
(1)求∠DBC的度数.
(2)猜想△BCD的形状并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com