
”¾ĢāÄæ”æĪŅĆĒŌ¼¶Ø£ŗČē¹ūÉķøßŌŚŃ”¶Ø±ź×¼µÄ”Ą2%·¶Ī§Ö®ÄŚ¶¼³ĘĪŖ”°ĘÕĶØÉķøß”±£®ĪŖĮĖĮĖ½āijŠ£¾ÅÄź¼¶ÄŠÉśÖŠ¾ßÓŠ”°ĘÕ±éÉķøß”±µÄČĖŹż£¬ĪŅĆĒ“ÓøĆŠ£¾ÅÄź¼¶ÄŠÉśÖŠĖ껜³é³ö10ĆūÄŠÉś£¬·Ö±š²āĮæ³öĖūĆĒµÄÉķøߣص„Ī»£ŗcm£©£¬ŹÕ¼Æ²¢ÕūĄķČēĻĀĶ³¼Ę±ķ£ŗ

£Ø1£©¼ĘĖćÕā×鏿¾ŻµÄČżøöĶ³¼ĘĮæ£ŗĘ½¾łŹż”¢ÖŠĪ»Źż”¢ÖŚŹż£»
£Ø2£©ĒėÄćŃ”ŌńĘäÖŠŅ»øöĶ³¼ĘĮæ×÷ĪŖŃ”¶Ø±ź×¼£¬ÕŅ³öÕā10ĆūÄŠÉśÖŠ¾ßÓŠ”°ĘÕ±éÉķøß”±ŹĒÄļøĪ»ÄŠÉś£æ²¢ĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©Ę½¾łŹżĪŖ166.6cm£¬ÖŠĪ»Źż165cm£¬ÖŚŹż£ŗ164cm£Ø2£©¼ū½āĪö
”¾½āĪö”æ
£Ø1£©Ę½¾łŹżĪŖ£ŗ
![]() =166.6£Øcm£©£»
=166.6£Øcm£©£»
10ĆūĶ¬Ń§Éķøß“ÓŠ”µ½“óÅÅĮŠČēĻĀ£ŗ
159”¢161”¢163”¢164”¢164”¢166”¢169”¢171”¢173”¢174£¬
ÖŠĪ»Źż£ŗ![]() =165£Øcm£©£»
=165£Øcm£©£»
ÖŚŹż£ŗ164£Øcm£©£»
£Ø2£©Ń”Ę½¾łŹż×÷ĪŖ±ź×¼£ŗ
ÉķøßxĀś×ć166.4”Į£Ø1©2%£©”Üx”Ü166.4”Į£Ø1+2%£©
¼“163.072”Üx”Ü169.728Ź±ĪŖĘÕ±éÉķøߣ¬
“ĖŹ±¢ß¢ą¢į¢āÄŠÉśµÄÉķøß¾ßÓŠ”°ĘÕ±éÉķøß”±£®
є֊Ī»Źż×÷ĪŖ±ź×¼£ŗ
ÉķøßxĀś×ć165”Į£Ø1©2%£©”Üx”Ü165”Į£Ø1+2%£©
¼“161.7”Üx”Ü168.3Ź±ĪŖĘÕ±éÉķøߣ¬“ĖŹ±¢Ł¢ß¢ą¢āÄŠÉśµÄÉķøß¾ßÓŠ”°ĘÕ±éÉķøß”±£®
є֌Źż×÷ĪŖ±ź×¼£ŗ
ÉķøßxĀś×ć164”Į£Ø1©2%£©”Üx”Ü164”Į£Ø1+2%£©
¼“160.72”Üx”Ü167.28Ź±ĪŖĘÕ±éÉķøߣ¬“ĖŹ±¢Ł¢Ż¢ß¢ą¢āÄŠÉśµÄÉķøß¾ßÓŠ”°ĘÕ±éÉķøß”±£®
£Ø1£©øł¾ŻĘ½¾łŹż”¢ÖŠĪ»Źż”¢ÖŚŹżµÄ¶ØŅå½ųŠŠ¼ĘĖć¼“æÉµĆ½ā£»
£Ø2£©øł¾Ż£Ø1£©ÖŠĒó³öµÄŹż¾Ż£¬Ēó³öĘÕ±éÉķøßµÄȔֵ·¶Ī§£¬Č»ŗóČ·¶ØѧɜŠņŗż“æÉ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻBAC£½90”ć£¬AB£½AC£¬µćDĪŖÖ±ĻßBCÉĻŅ»¶Æµć£ØµćD²»ÓėB”¢CÖŲŗĻ£©£¬ŅŌADĪŖÖ±½Ē±ßŌŚADÓŅ²ą×÷µČŃüÖ±½ĒČż½ĒŠĪADE£¬ĒŅ”ĻDAE£½90”ć£¬Į¬½ÓCE£®
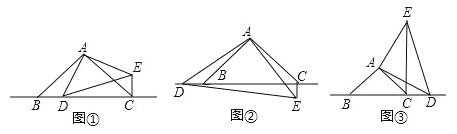
£Ø1£©ČēĶ¼¢Ł£¬µ±µćDŌŚĻ߶ĪBCÉĻŹ±£ŗ
¢ŁBCÓėCEµÄĪ»ÖĆ¹ŲĻµĪŖ”” ””£»
¢ŚBC”¢CD”¢CEÖ®¼äµÄŹżĮæ¹ŲĻµĪŖ”” ””£®
£Ø2£©ČēĶ¼¢Ś£¬µ±µćDŌŚĻ߶ĪCBµÄŃÓ³¤ĻßÉĻŹ±£¬½įĀŪ¢Ł£¬¢ŚŹĒ·ńČŌČ»³ÉĮ¢£æČō²»³ÉĮ¢£¬ĒėÄ抓³öÕżČ·½įĀŪ£¬²¢øųÓčÖ¤Ć÷£®
£Ø3£©ČēĶ¼¢Ū£¬µ±µćDŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻŹ±£¬BC”¢CD”¢CEÖ®¼äµÄŹżĮæ¹ŲĻµĪŖ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»ø±Ö±½ĒČż½Ē°åµž·ÅŌŚŅ»ĘšæÉŅŌĘ“³ö¶ąÖÖĶ¼ŠĪ£¬ČēĶ¼¢Ł”Ŗ¢Ü£¬Ćæ·łĶ¼ÖŠĖłĒó½Ē¶ČÕżČ·µÄøöŹżÓŠ£Ø £©
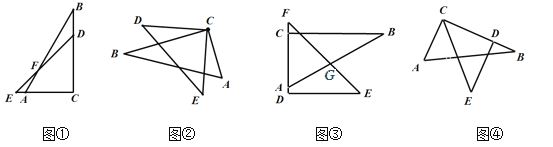
¢Ł”ĻBFD=15”ć£»¢Ś”ĻACD+”ĻECB=150”ć£»¢Ū”ĻBGE=45”ć £»¢Ü”ĻACE=30”ć
A.1øöB.2øöC.3øöD.4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹«Ė¾33ĆūÖ°¹¤µÄŌĀ¹¤×Ź(µ„Ī»£ŗŌŖ)ČēĻĀ£ŗ
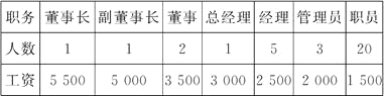
(1)ĒóøĆ¹«Ė¾Ö°¹¤ŌĀ¹¤×ŹµÄĘ½¾łŹż”¢ÖŠĪ»Źż”¢ÖŚŹż£»(¾«Č·µ½øöĪ»)
(2)¼ŁÉčø±¶ŹĀ³¤µÄ¹¤×Ź“Ó5 000ŌŖĢįÉżµ½20 000ŌŖ£¬¶ŹĀ³¤µÄ¹¤×Ź“Ó5 500ŌŖĢįÉżµ½30 000ŌŖ£¬ÄĒĆ“ŠĀµÄĘ½¾łŹż”¢ÖŠĪ»Źż”¢ÖŚŹżÓÖø÷ŹĒ¶ąÉŁ£æ(¾«Č·µ½øöĪ»)
(3)ÄćČĻĪŖÄÄøöĶ³¼ĘĮæøüÄÜ·“Ó³Õāøö¹«Ė¾Ö°¹¤µÄ¹¤×ŹĖ®Ę½,²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABC ÖŠ£¬µć D£¬E ·Ö±šŌŚ±ß AC£¬AB ÉĻ£¬BD Óė CE ½»ÓŚµć O£¬øų³öĻĀĮŠČżøöĢõ¼ž£ŗ¢Ł”ĻEBO£½”ĻDCO£»¢ŚBE£½CD£»¢ŪOB£½OC£®
(1)ÉĻŹöČżøöĢõ¼žÖŠ£¬ÓÉÄÄĮ½øöĢõ¼žæÉŅŌÅŠ¶Ø”÷ABC ŹĒµČŃüČż½ĒŠĪ£æ(ÓĆŠņŗÅŠ“³öĖłÓŠ³ÉĮ¢µÄĒéŠĪ)
(2)ĒėŃ”Ōń(1)ÖŠµÄŅ»ÖÖĒéŠĪ£¬Š“³öÖ¤Ć÷¹ż³Ģ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖ½ųŠŠÓšĆ«Ēņ±ČČü£¬ÓšĆ«Ēņ·ÉŠŠµÄĀ·ĻßĪŖÅ×ĪļĻßµÄŅ»²æ·Ö£¬ČēĶ¼£¬¼×ŌŚ ![]() µćÉĻÕż·½
µćÉĻÕż·½ ![]() µÄ
µÄ ![]() “¦·¢³öŅ»Ēņ£¬ÓšĆ«Ēņ·ÉŠŠµÄø߶Č
“¦·¢³öŅ»Ēņ£¬ÓšĆ«Ēņ·ÉŠŠµÄøß¶Č ![]() ÓėĖ®Ę½¾ąĄė
ÓėĖ®Ę½¾ąĄė ![]() Ö®¼äĀś×ćŗÆŹż±ķ“ļŹ½
Ö®¼äĀś×ćŗÆŹż±ķ“ļŹ½ ![]() £®ŅŃÖŖµć
£®ŅŃÖŖµć ![]() ÓėĒņĶųµÄĖ®Ę½¾ąĄėĪŖ
ÓėĒņĶųµÄĖ®Ę½¾ąĄėĪŖ ![]() £¬ĒņĶųµÄø߶ČĪŖ
£¬ĒņĶųµÄø߶ČĪŖ ![]() £®
£®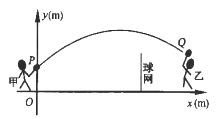
£Ø1£©µ± ![]() Ź±£¬¢ŁĒó
Ź±£¬¢ŁĒó ![]() µÄÖµ£»¢ŚĶعż¼ĘĖćÅŠ¶Ļ“ĖĒņÄÜ·ń¹żĶų£»
µÄÖµ£»¢ŚĶعż¼ĘĖćÅŠ¶Ļ“ĖĒņÄÜ·ń¹żĶų£»
£Ø2£©Čō¼×·¢Ēņ¹żĶųŗó£¬ÓšĆ«Ēņ·ÉŠŠµ½ ![]() “¦Ź±,ŅŅæŪĒņ³É¹¦”£ŅŃÖŖµć
“¦Ź±,ŅŅæŪĒņ³É¹¦”£ŅŃÖŖµć ![]() Ąėµć
Ąėµć ![]() µÄĖ®Ę½¾ąĄėĪŖ
µÄĖ®Ę½¾ąĄėĪŖ ![]() £¬ĄėµŲĆęµÄø߶ČĪŖ
£¬ĄėµŲĆęµÄø߶ČĪŖ ![]() µÄ£¬Ēó
µÄ£¬Ēó ![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćCŌŚĻ߶ĪABÉĻ£¬”÷DACŗĶ”÷DBE¶¼ŹĒµČ±ßČż½ĒŠĪ£® 
£Ø1£©ĒóÖ¤£ŗ”÷DAB”Õ”÷DCE£»
£Ø2£©ĒóÖ¤£ŗDA”ĪEC£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĖıߊĪABCDµÄ¶Ō½ĒĻßACÓėBD½»ÓŚµćO£¬øų³öĻĀĮŠĖÄøöĀŪ¶Ļ£ŗ
¢ŁOA=OC£¬¢ŚAB=CD£¬¢Ū”ĻBAD=”ĻDCB£¬¢ÜAD”ĪBC£®
ĒėÄć“ÓÖŠŃ”ŌńĮ½øöĀŪ¶Ļ×÷ĪŖĢõ¼ž£¬ŅŌ”°ĖıߊĪABCDĪŖĘ½ŠŠĖıߊĪ”±×÷ĪŖ½įĀŪ£¬Ķź³ÉĻĀĮŠø÷Ģā£ŗ
£Ø1£©¹¹ŌģŅ»øöÕęĆüĢā£¬»Ķ¼²¢øų³öÖ¤Ć÷£»
£Ø2£©¹¹ŌģŅ»øö¼ŁĆüĢā£¬¾Ł·“Ąż¼ÓŅŌĖµĆ÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻBAC=90”ć£¬AC=2AB£¬µćDŹĒACµÄÖŠµć£®½«Ņ»æéČń½ĒĪŖ45”ćµÄÖ±½ĒČż½Ē°åČēĶ¼·ÅÖĆ£¬Ź¹Čż½Ē°åŠ±±ßµÄĮ½øö¶Ėµć·Ö±šÓėA”¢DÖŲŗĻ£¬Į¬½ÓBE”¢EC£®
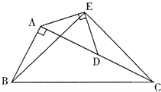 ŹŌ²ĀĻėĻ߶ĪBEŗĶECµÄŹżĮæ¼°Ī»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®
ŹŌ²ĀĻėĻ߶ĪBEŗĶECµÄŹżĮæ¼°Ī»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com