
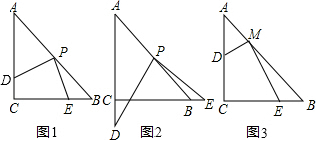
分析 (1)因为△ABC是等腰直角三角形,所以连接PC,容易得到△ACP、△CPB都是等腰直角三角形.连接CP,就可以证明△CDP≌△BEP,再根据全等三角形的对应边相等,就可以证明DP=PE;
(2)△PBE能成为等腰三角形,位置有四种;
(3)作MH⊥CB,MF⊥AC,构造相似三角形△MDF和△MHE,然后利用对应边成比例,就可以求出MD和ME之间的数量关系.
解答 解:(1)猜想:PD=PE
理由:如图1中,连接PC.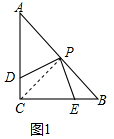
∵△ABC是等腰直角三角形,P是AB的中点,
∴CP=PB,CP⊥AB,∠ACP=$\frac{1}{2}$∠ACB=45°.
∴∠ACP=∠B=45°.
又∵∠DPC+∠CPE=∠BPE+∠CPE=90°,
∴∠DPC=∠BPE.
∴△PCD≌△PBE.
∴PD=PE;
如图2中,结论一样,证明方法类似;
(2)共有四种情况:
①当点C与点E重合,即CE=0时,PE=PB;
②CE=2-$\sqrt{2}$,此时PB=BE;
③当CE=1时,此时PE=BE;
④当E在CB的延长线上,且CE=2+$\sqrt{2}$时,此时PB=EB;
(3)结论:MD:ME=1:3.
理由:过点M作MF⊥AC,MH⊥BC,垂足分别是F、H.
∴MH∥AC,MF∥BC.
∴四边形CFMH是平行四边形.
∵∠C=90°,
∴?CFMH是矩形.
∴∠FMH=90°,MF=CH.
∵$\frac{CH}{HB}$=$\frac{AM}{MB}$=$\frac{1}{3}$,HB=MH,
∴$\frac{MF}{MH}$=$\frac{1}{3}$.
∵∠DMF+∠DMH=∠DMH+∠EMH=90°,
∴∠DMF=∠EMH.
∵∠MFD=∠MHE=90°,
∴△MDF∽△MEH.
∴$\frac{MD}{ME}$=$\frac{MF}{MH}$=$\frac{1}{3}$.
点评 此题比较复杂,综合考查全等三角形的判定与性质、相似三角形的判定与性质、矩形的判定与性质、图形的变换.综合性很强,勾股定理的计算要求也比较高.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
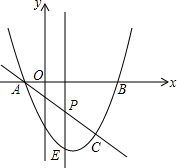 如图,抛物线y=x2-2x-3与x轴交于A,B两点(点A在点B的左侧),直线y=kx+b与抛物线交于A,C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交于A,B两点(点A在点B的左侧),直线y=kx+b与抛物线交于A,C两点,其中C点的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com