
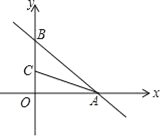
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
【答案】C
【解析】
过C作CD⊥AB于D,先求出A,B的坐标,分别为A(8,0),B(0,6),得到AB的长,再根据折叠的性质得到AC平分∠OAB,得到CD=CO=n,DA=OA=8,则DB=10-8=2,BC=6-n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.
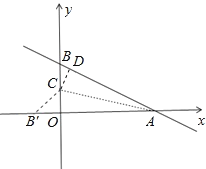
过C作CD⊥AB于D,如图,
对于直线y=![]() x+6,
x+6,
当x=0,得y=6;当y=0,x=8,
∴A(8,0),B(0,6),即OA=8,OB=6,
∴AB=10,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=6n,
∴DA=OA=8,
∴DB=108=2,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+22=(6n)2,解得n=![]() ,
,
∴点C的坐标为(0,![]() ).
).
故选:C.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.

(2)结论应用:① 如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正△ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求旋转角的度数;
(2)求点P与点P′之间的距离;
(3)求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解参加某校运动会的![]() 名运动员的年龄情况,从中抽取了
名运动员的年龄情况,从中抽取了![]() 名运动员的年龄,就这个问题,下面说法正确的是( )
名运动员的年龄,就这个问题,下面说法正确的是( )
A. ![]() 名运动员是总体 B. 每个运动员是个体
名运动员是总体 B. 每个运动员是个体
C. 抽取的![]() 名运动员是样本 D. 每个运动员的年龄是个体
名运动员是样本 D. 每个运动员的年龄是个体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①两个数互为倒数,则它们的乘积为![]() ;②若
;②若![]() ,
,![]() 互为相反数,则
互为相反数,则![]() ;
;
③![]() 个有理数相乘,如果负因数的个数为奇数个,则积为负;④若
个有理数相乘,如果负因数的个数为奇数个,则积为负;④若![]() ,则
,则![]() .其中正确的个数为( )
.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式 | 批发 | 零售 | 储藏后销售 |
售价(元/吨) | 3000 | 4500 | 5500 |
成本(元/吨) | 700 | 1000 | 1200 |
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的![]() .
.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三点,分别表示有理数-26、-10、10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:PA=________,PC=_____________
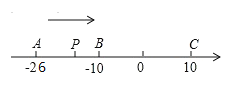
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,当点Q开始运动后,请用t的代数式表示P、Q两点间的距离。(友情提醒:注意考虑P、Q的位置)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com