
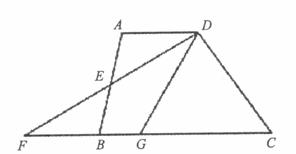
如图所示,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在BC边上,且∠GDF=∠ADF。
(1)求证:△ADE≌ABFE
(2)连接EG,判断EG与DF的位置关系,并说明理由。

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了120米到达B处,测的∠CBN=70°,
求河流的宽度CE(结果保留两个有效数字).
(参考数据:
sin35°≈0.57,cos35°≈0.82,tan35°≈0.70
Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,工人师傅要在墙壁的O处用钻打孔, 要使孔口从墙壁对面的B点处打开,墙壁厚是35 cm,B点与O点的铅直距离AB长是20 cm,工人师傅在旁边墙上与AO水平的线上截取OC=35 cm,画CD⊥OC,使CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请你说出理由.
要使孔口从墙壁对面的B点处打开,墙壁厚是35 cm,B点与O点的铅直距离AB长是20 cm,工人师傅在旁边墙上与AO水平的线上截取OC=35 cm,画CD⊥OC,使CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请你说出理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线 与双曲线
与双曲线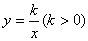 交于
交于 、
、 两
两 点,
点, 点横坐标为4.
点横坐标为4.
(1)求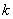 值;
值;
(2)直接写出关于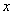 的不等式
的不等式 的解集;
的解集;
(3)若双曲线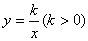 上有一点
上有一点 的纵坐标为8,求△
的纵坐标为8,求△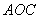 的面积.
的面积.
(4)若在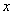 轴上有点
轴上有点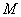 ,
, 轴上有点
轴上有点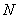 ,且点
,且点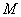 、
、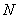 、
、 、
、 四点恰好构成平行四边形,直接写出点
四点恰好构成平行四边形,直接写出点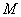 、
、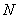 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com