
【题目】探究:
(1)如图①,在等腰直角三角形ABC中,∠ACB=90,作CM平分∠ACB交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD、BE
填空:
①线段BD、BE的数量关系为______.
②线段BC、DE的位置关系为______.
推广:
(2)如图②,在等腰三角形ABC中,顶角∠ACB=a,作CM平分∠ACB交AB于点M,点D为△ABC外部射线CM上一点,以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE、BD、BE请判断(1)中的结论是否成立,并说明理由.
应用:
(3)如图③,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,请直接写出DE的值.

【答案】(1)①BD=CE;②BD⊥CE;(2)结论:(1)中的结论仍然成立,理由见解析;(3)满足条件的DE的值为![]() 或4
或4![]() .
.
【解析】
①由CA=CB,∠ACB=90°,CM平分∠ACB,得出∠ECF=∠DCF=45°,易证△CBD≌△CBE,即可得出BD=BE;
②由CD=CE即可得出BC⊥DE.
(2)由CA=CB,∠ACB=α,CM平分∠ACB,得出∠ECF=∠DCF=![]() α,易证△CBD≌△CBF,即可得出BD=BE,再由等腰三角形的性质得出BC⊥DE.
α,易证△CBD≌△CBF,即可得出BD=BE,再由等腰三角形的性质得出BC⊥DE.
(3)分两种情况,根据三角形全等的性质及三角函数即可得出.
(1)如图①中,
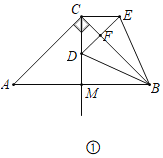
∵CA=CB,∠ACB=90°,CM平分∠ACB,
∴∠ACM=∠BCM=45°,
∵∠ECD=90°,
∴∠ECF=∠DCF=45°,
∵CD=CE,CB=CB,
∴△CBD≌△CBE(SAS),
∴BD=BE,
∵CD=CE,
∴BC垂直平分线段DE,
∴BC⊥DE.
故答案为BD=CE,BD⊥CE.
(2)结论:(1)中的结论仍然成立.
理由:如图②中,
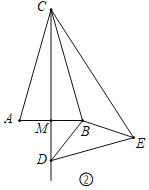
∵CA=CB,∠ACB=α,CM平分∠ACB,
∴∠ACM=∠BCM=![]() α,
α,
∵∠ECD=α,
∴∠ECF=∠DCF=![]() α,
α,
∵CD=CE,CB=CB,
∴△CBD≌△CBF(SAS),
∴BD=BE,
∵CD=CE,
∴BC垂直平分线段DE,
∴BC⊥DE.
(3)如图③中,
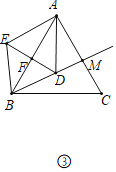
当△AFE≌△AMD时,AF=AM,
∵∠AFD=∠AMD=90°,
∵AD=AD,
∴Rt△ADF≌Rt△ADM(HL),
∴∠DAF=∠DAM=30°,
∴∠DBA=∠DAB=30°,
∴DA=DB,
∵DF⊥AB,
∴∠BDF=60°,BF=AF=2,
∵BD=BE,
∴△BDE是等边三角形,
∴DF=EF=BFtan30°=![]() ,
,
∴DE=2EF=![]() .
.
如图③-1中,当点D在AM的延长线时,易证AF=AM=2,DE=2DF=4![]() .
.
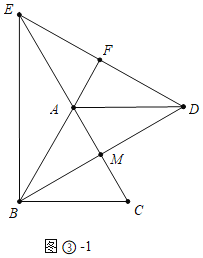
综上所述,满足条件的DE的值为![]() 或4
或4![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(根) | 40 | 30 | 24 | 20 |
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
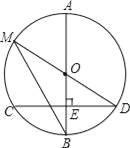
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】众所周知,水的污染越来越严重,日益影响着人类的身心健康,而人们的安全饮水意识仍有待提高.已知某品牌型号Ⅰ净水器的市场售价为2000元/台,型号Ⅱ净水器的市场售价为1800元/台.为了保护我区市民的安全饮水,推动北碚区创建国家级卫生区复审工作,启动了“安全饮水北碚行”活动,此两种型号的净水器可获得13%的财政补贴.
(1)某商场在启动活动前一个月共售出此两种净水器960台,启动活动后的第一个月型号Ⅰ和型号Ⅱ净水器的销量分别比上月增长30%、25%,这个月这两种净水器共售出1228台.启动活动前一个月此两种型号的净水器销量各为多少台?
(2)在启动活动前区政府打算用25000元为天府镇敬老院购买该两种型号的净水器,并计划恰好全部用完此款.
①原计划所购买的型号Ⅰ和型号Ⅱ净水器各多少台?
②活动启动后,在不增加区政府实际负担的情况下,能否多购买两台型号Ⅱ净水器?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场经销龟苓膏粉,其中![]() 品牌的批发价是每包20元,
品牌的批发价是每包20元,![]() 品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
(1)若购买这些龟苓膏粉共花费22000元,求两种品牌的龟苓膏粉各购买了多少包?
(2)若凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元,
若购买会员卡并用此卡购买这些龟苓膏粉共花费![]() 元,设
元,设![]() 品牌购买了
品牌购买了![]() 包,请求出
包,请求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
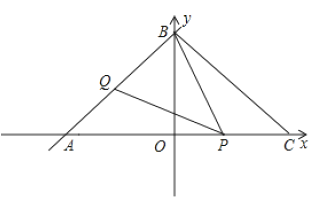
【题目】如图,一次函数![]() 的图象与
的图象与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.动点
轴对称.动点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上(点
上(点![]() 与点
与点![]() ,
,![]() 不重合),且满足
不重合),且满足![]() .
.
(1)求点![]() ,
,![]() 的坐标及线段
的坐标及线段![]() 的长度;
的长度;
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由;
,说明理由;
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求出售价x的范围;
(3)商场每月销售这种空气净化器所获得的利润为w(元),写出w关于x的关系?当售价x(元/台)定为多少时利润最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在干燥的路面上,使车子停止前进所需的刹车距离s(m)与车速v(km/h)的关系是s=![]() v+
v+![]() v2 .
v2 .
(1)当v分别是48,64时,求相应的刹车距离s的值;
(2)司机小李正以72km/h的速度行驶,突然发现前方大约60m处有一不明障碍物,他立即刹车,车会撞上障碍物吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com