
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用全等三角形的判定定理分别判断后即可确定正确的选项.
解答 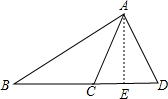 解:有两边和其中一边上的中线对应相等的两个三角形全等,所以①正确.有两边和第三边上的中线对应相等的两个三角形全等,所以②正确;
解:有两边和其中一边上的中线对应相等的两个三角形全等,所以①正确.有两边和第三边上的中线对应相等的两个三角形全等,所以②正确;
有两边和这两边夹角的平分线对应相等的两个三角形全等,所以③正确;
如图,在△ABC和△ABD中,AB公共,AC=AD,高AE公共,但是△ABC和△ABD不全等,故④错误.
故选C.
点评 此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:选择题
| A. | (-3,-5)(3,5) | B. | (-3,5)(3,-5) | C. | (3,5)(-3,-5) | D. | (3,-5)(-3,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
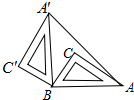 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )| A. | 10$\sqrt{2}$ | B. | 10 | C. | 20 | D. | 5$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿AB向点B以1cm/s的速度移动,同时点Q从点B沿BC向点C以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿AB向点B以1cm/s的速度移动,同时点Q从点B沿BC向点C以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
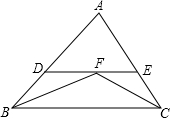 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )| A. | 2014 | B. | 2011 | C. | 2012 | D. | 2013 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com