
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
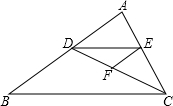 如图,已知三角形ABC,点D、E分别在线段AB、AC上,连结DE、CD,F为线段CD上一点,连结EF.∠EFC+∠BDC=180°,∠DEF=∠B,试判断DE与BC的位置关系,并说明理由.
如图,已知三角形ABC,点D、E分别在线段AB、AC上,连结DE、CD,F为线段CD上一点,连结EF.∠EFC+∠BDC=180°,∠DEF=∠B,试判断DE与BC的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
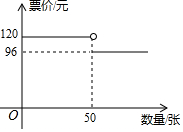 某旅游景点每张普通门票的票价与买票的数量之间的函数关系如图所示.
某旅游景点每张普通门票的票价与买票的数量之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com