
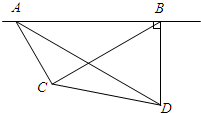
 如图,在我市的上空一架飞机由A向B沿水平直线方向飞行,沿航线AB的正下方有两个景点水城明珠大剧院(记为点C),光岳楼(记为点D),飞机在A处时,测得景点C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了3千米到B处时,往后测得景点C的俯角为30°.而景点D恰好在飞机的正下方,求水城明珠大剧院与光岳楼之间的距离(最后结果精确到0.1千米)
如图,在我市的上空一架飞机由A向B沿水平直线方向飞行,沿航线AB的正下方有两个景点水城明珠大剧院(记为点C),光岳楼(记为点D),飞机在A处时,测得景点C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了3千米到B处时,往后测得景点C的俯角为30°.而景点D恰好在飞机的正下方,求水城明珠大剧院与光岳楼之间的距离(最后结果精确到0.1千米) 分析 首先证明△ABC是直角三角形,分别在RT△ABC,RT△ABD中求出BC、BD、BE,再在RT△CDE中利用勾股定理即可解决问题.
解答 解:由题意,∠BAC=60°,∠ABC=30°,∠BAD=90°,
∴∠ACB=180°-∠ABC-∠BAC=180°-30°-60°=90°,
∴在RT△ABC中,BC=AB•cos30°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$(千米),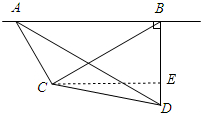
在RT△ABD中,BD=AB•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$(千米),
过点C作CE⊥BD于点E,
∵AB⊥BD,∠ABC=30°,
∴∠CBE=60°,
∴BE=BC•cos60°=$\frac{3\sqrt{3}}{2}$×$\frac{1}{2}$=$\frac{3\sqrt{3}}{4}$,
DE=BD-BE=$\sqrt{3}$-$\frac{3\sqrt{3}}{4}$=$\frac{\sqrt{3}}{4}$,
CE=BC•sin60°=$\frac{3\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{9}{4}$,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{(\frac{\sqrt{3}}{4})^{2}+(\frac{9}{4})^{2}}$=$\frac{1}{2}$$\sqrt{21}$≈2.3(千米).
点评 本题考查解直角三角形应用-俯角俯角、三角函数、勾股定理等知识,解题的关键是添加辅助线构造直角三角形,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+$\frac{7}{2}$a+m)(a为任意实数)在抛物线上,直线y=kx+b经过A、B两点,平行于y轴的直线x=2交AB于点D,交抛物线于点E.
如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+$\frac{7}{2}$a+m)(a为任意实数)在抛物线上,直线y=kx+b经过A、B两点,平行于y轴的直线x=2交AB于点D,交抛物线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
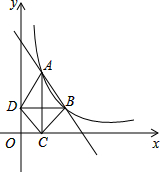 如图,在平面直角坐标xOy内,函数y=$\frac{m}{x}$(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB.
如图,在平面直角坐标xOy内,函数y=$\frac{m}{x}$(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com