
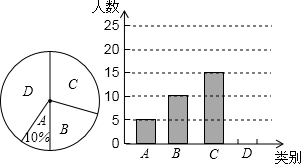
分析 (1)由A类5人,占10%,可求得总人数,继而求得B类别占的百分数,则可求得“B类别”的扇形的圆心角的度数;
(2)首先求得D类别的人数,则可将条形统计图补充完整;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他们同时选中古隆中的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵A类5人,占10%,
∴八(1)班共有学生有:5÷10%=50(人);
∴在扇形统计图中,表示“B类别”的扇形的圆心角的度数为:$\frac{10}{50}$×360°=72°;
故答案为:50,72°;
(2)D类:50-5-10-15=20(人),如图: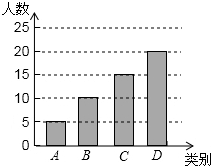
(3)分别用1,2,3表示古隆中、习家池、鹿门寺,画树状图得: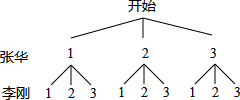
∵共有9种等可能的结果,他们同时选中古隆中的只有1种情况,
∴他们同时选中古隆中的概率为:$\frac{1}{9}$.
故答案为:$\frac{1}{9}$.
点评 此题考查了列表法或树状图法求概率以及扇形与条形统计图的知识.注意掌握扇形统计图与条形统计图的对应关系.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
 如图,将△ABC绕点A逆时针旋转得到△AB′C′,若B′落到BC边上,∠B=50°,则∠CB′C′的度数为( )
如图,将△ABC绕点A逆时针旋转得到△AB′C′,若B′落到BC边上,∠B=50°,则∠CB′C′的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9天 | B. | 11天 | C. | 13天 | D. | 22天 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
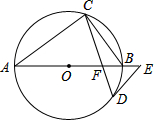 如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC.
如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com