
 如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.分析 (1)根据函数图象和题意可以直接得到当x取何值时,y1>y2;
(2)根据题意可以得到反比例函数的解析式和点C平移后的坐标,从而可以解答本题.
解答 解:(1)由函数图象可得,
当x>1时,y1>y2;
(2)∵BC⊥x轴,垂足为C,且OC=1
∴C(1,0),点B的横坐标为1,
当x=1时,y1=x+1=2,
∴B(1,2),
∵点B在反比例函数的图象上
∴$2=\frac{k}{1}$,
∴k=2,
由y1=x+1=0,解得x=-1,
∴A(-1,0),
∴将线段BC沿一次函数的图象平移至点B与点A重合时,线段BC向下平移了2个单位,向左平移了2个单位,平移后点C的对应点的坐标为(-1,-2),
当x=-1时,${y_2}=\frac{2}{-1}=-2$,
∴平移后点C的对应点在反比例函数的图象上.
点评 本题考查反比函数与一次函数的交点问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用反比例函数的性质与数形结合的思想解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
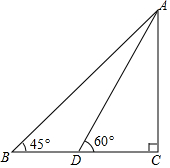 如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
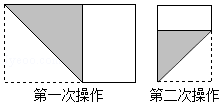 长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值.
长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
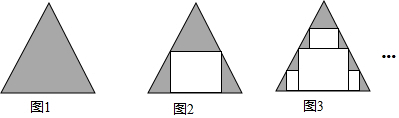
| A. | $\frac{\sqrt{3}}{{2}^{n-1}}{a}^{2}$ | B. | $\frac{\sqrt{3}}{{2}^{n}}{a}^{2}$ | C. | $\frac{\sqrt{3}}{{2}^{n+1}}{a}^{2}$ | D. | $\frac{\sqrt{3}}{{2}^{n+2}}{a}^{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1≤y2 | C. | y1>y2 | D. | y1≥y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com