
如图,把双曲线 (虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
(虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
①双曲线C2是中心对称图形,其对称中心是(2,0).
②双曲线C2仍是轴对称图形,它有两条对称轴.
③双曲线C2与y轴有交点,与x轴也有交点.
④当x<2时,双曲线C2中的一支,y的值随着x值的增大而减小.其中正确结论的序号是 _________ .(多填或错填得0分,少填则酌情给分.)
①②④
【解析】
试题分析:先根据平移的性质得出双曲线C2的解析式,再根据双曲线的特点对四个小题进行逐一分析.
解:∵双曲线C2是双曲线y= 沿x轴的正方向、向右平移2个单位得到的,
沿x轴的正方向、向右平移2个单位得到的,
∴此双曲线的解析式为:y= ,
,
∵原双曲线的对称中心为(0,0),所以新双曲线的对称中心也沿x轴向右移动2个单位,其坐标为(2,0),故①正确;
∵图形平移后其性质不会改变,
∴双曲线C2仍是轴对称图形,它有两条对称轴,故②正确;
∵反比例函数的图象与两坐标轴永远没有交点,
∴双曲线C2与y轴没有交点,与x轴也没有交点,故③错误;
∵当x<2时,双曲线C2中的一支在第三象限,
∴y的值随着x值的增大而减小,故④正确.
故答案为:①②④.
考点:反比例函数的性质.
点评:本题考查的是反比例函数的性质及平移的性质,熟知反比例函数的性质是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2013年初中数学单元提优测试卷-反比例函数的性质、k的几何意义(带解析) 题型:填空题
如图,把双曲线 (虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
(虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
①双曲线C2是中心对称图形,其对称中心是(2,0).
②双曲线C2仍是轴对称图形,它有两条对称轴.
③双曲线C2与y轴有交点,与x轴也有交点.
④当x<2时,双曲线C2中的一支,y的值随着x值的增大而减小.其中正确结论的序号是 _________ .(多填或错填得0分,少填则酌情给分.)
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江西省抚州市临川区罗湖中学九年级(上)第三次月考数学试卷(解析版) 题型:填空题
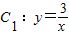 (虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
(虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
查看答案和解析>>
科目:初中数学 来源:2011年江西省赣州市中考适应性考试数学试卷(解析版) 题型:填空题
 (虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
(虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
查看答案和解析>>
科目:初中数学 来源:2011年江西省中考数学模拟试卷(B)(解析版) 题型:填空题
 (虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
(虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com