Question

解下列不等式，并把解集表示在数轴上：
（1）3x-2＜5x+4；
（2）10-4（x-3）≤3（x-2）；
（3）x-

3x-5

2

≤

2(8-x)

5

-1；
（4）

5x-(x-2)＞6 -4(2x+1)＜12(1-x)

；
（5）

x+y=6 x+z=7 y+z=9

；
（6）

3(1-x)≥2(x+9) x-3 0.5 - x+4 0.2 ＜-14

．

Answer 1

分析：分别解出两个不等式的解集，然后确定解集的公共部分就可以求出不等式的解集．

解答：（1）解：原式得3x-5x＜4+2（1分）
-2x＜6（2分）
x＞-3．（4分）
（5分）

（2）解：原式得10-4x+12≤3x-6（1分）
-4x-3x≤-6-10-12（2分）
-7x≤-28（3分）
x≥4．（4分）
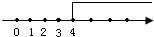
（5分）

（3）解：原式得10x-5（3x-5）≤4（8-x）-10
10x-15x+25≤32-4x-10（1分）
10x-15x+4x≤32-10-25（2分）
-x≤-3（3分）
x≥3．（4分）
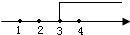
（5分）

（4）解：由①得5x-x+2＞6
x＞1（12分）
由①得-8x-4＜12-12x
x＜4（4分）
∴1＜x＜4．（4分）
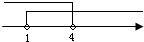
（5分）

（5）解：原式=①+②+③得
2x+2y+2z=22
x+y+z=11④（1分）
④-①得：x=5（2分）
④-②得：y=4（3分）
④-③得：z=2（4分）
∴

x=5 y=4 z=2

．（5分）


（6）由①得：3-3x≥2x+18
-3x-2x≥18-3
x≤-3（2分）
由②得：

10x-30

5

-

10x+40

2

≤-14
2（10x-30）-5（10x+40）≤-140
解得：x≥-4（4分）
∴-4≤x≤-3．（5分）

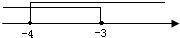
点评：不等式组解集确定的法则是：同大取大、同小取小、大小小大取中间，大大小小是无解．在数轴上的反映就是取它们都含有的公共部分．在解不等式时，注意没有分母的项不要漏乘．以及不等号的方向的变化．