
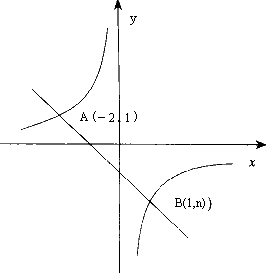
如下图,一次函数y=kx+b的图像与反比例函数y=![]() 的图像交于A、B两点,利用图中的条件,求这两个函数的解析式.
的图像交于A、B两点,利用图中的条件,求这两个函数的解析式.
|
简解:由图知双曲线经过点A(-2,1), ∴ ∴反比例函数解析式为y=- 又双曲线线经过点B, ∴- ∵直线y=kx+b经过点A、B, ∴ ∴一次函数的解析式为y=-x-1. 二次函数的解析式有三种求解形式,一般地,当已知二次函数图像上三个点的坐标时,宜用一般式y=ax2+bx+c求解;当已知二次函数图像的顶点坐标和图像上另一个点的坐标时,宜用顶点式y=a(x-h)2+k求解;当已知二次函数图像与x轴两个交点的横坐标和图像上其他一点的坐标时,宜用双根式y=a(x-x1)(x-x2)求解,有的题可同时用这三种形式求解,这在前面的数形结合思想中已有介绍,下面看两道较为综合的题目. 分析:因反比例函数y= |


科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
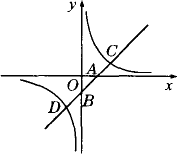
如下图,一次函数的图像与x轴、y轴分别交于A、B两点,与反比例函数的图像交于C、D两点.如果A点的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD.
试求一次函数和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:044
如下图,一次函数y=kx+b的图像与反比例函数y= 的图像交于A、B两点.(1)利用图中的条件,求两个函数的表达式;(2)根据图像写出使一次函数的值大于反比例函数的值的x的取值范围.
的图像交于A、B两点.(1)利用图中的条件,求两个函数的表达式;(2)根据图像写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源:2009年重庆市綦江县中考数学试卷 题型:044
如下图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象相交于A、B两点.
的图象相交于A、B两点.
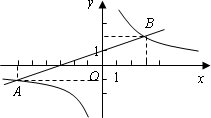
(1)根据图象,分别写出点A、B的坐标;
(2)求出这两个函数的解析式.
查看答案和解析>>
科目:初中数学 来源:2006年湖南省常德市初中毕业生学业考试数学试卷 题型:044
如下图,已知反比例函数y1=![]() (m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.
(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.
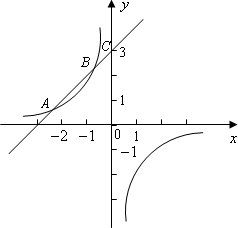
(1)分别求出反比例函数与一次函数的解析式;
(2)求点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com