
【题目】一只不透明的袋子中装有![]() 个大小、质地都相同的乒乓球,球面上分别标有数字
个大小、质地都相同的乒乓球,球面上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() ,搅匀后先从中摸出一个球(不放回),再从余下的
,搅匀后先从中摸出一个球(不放回),再从余下的![]() 个球中摸出
个球中摸出![]() 个球.
个球.
(1)用树状图列出所有可能出现的结果;
(2)求![]() 次摸出的乒乓球球面上数字的积为偶数的概率.
次摸出的乒乓球球面上数字的积为偶数的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC都是等边三角形,点E,F同时分别从点B,A出发,以相同的速度各自沿BA,AD的方向运动到点A,D停止,连结EC,FC.

(1)在点E,F运动的过程中,∠ECF的大小是否随之变化?请说明理由.
(2)在点E,F运动的过程中,以A,E,C,F为顶点的四边形的面积变化了吗?请说明理由.
(3)连结EF,在图中找出所有和∠ACE相等的角,并说明理由.
(4)若点E,F在射线BA,射线AD上继续运动下去,(1)中的结论还成立吗?直接写出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BD平分∠ABF,且交AE于点D.
(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);
(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
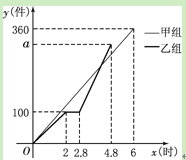
【题目】甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备
后,乙组的工作效率是原来的2倍.两组各自加工零件的数量![]() (件)与时间
(件)与时间![]() (时)的函数图
(时)的函数图
象如图所示.
(1)求甲组加工零件的数量y与时间![]() 之间的函数关系式.(2分)
之间的函数关系式.(2分)
(2)求乙组加工零件总量![]() 的值.(3分)
的值.(3分)
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?(5分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习等边三角形时发现了直角三角形的一个性质:直角三角形中,![]() 角所对的直角边等于斜边的一半。小明同学对以上结论作了进一步探究.如图1,在
角所对的直角边等于斜边的一半。小明同学对以上结论作了进一步探究.如图1,在![]() 中,
中,![]() ,则:
,则:![]() .
.
探究结论:(1)如图1,![]() 是
是![]() 边上的中线,易得结论:
边上的中线,易得结论:![]() 为________三角形.
为________三角形.
(2)如图2,在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是边
是边![]() 上任意一点,连接
上任意一点,连接![]() ,在
,在![]() 边上方作等边
边上方作等边![]() ,连接
,连接![]() .试探究线段
.试探究线段![]() 与
与![]() 之间的数量关系,写出你的猜想加以证明.
之间的数量关系,写出你的猜想加以证明.
拓展应用:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上的一动点,以
轴正半轴上的一动点,以![]() 为边作等边
为边作等边![]() ,当点
,当点![]() 在第一象内,且
在第一象内,且![]() 时,求点
时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
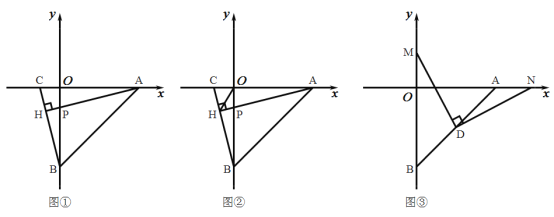
【题目】如图所示,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)如图①,若![]() 的坐标为
的坐标为![]() ,且
,且![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,试求点
,试求点![]() 的坐标;
的坐标;
(2)如图②,在(I)的条件下,连接![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() 点,当
点,当![]() 点在
点在![]() 轴正半轴上运动的过程中,式子
轴正半轴上运动的过程中,式子![]() 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】信息1:我们已经学完了解分式方程,它的一般步骤为:确定最简公分母、化为整式方程、求出整式方程的解、进行检验(第一,代入最简公分母验证是否为零,第二代入分式方程的左右两边检验是否相等)、确定分式方程的解.其中代入最简公分母验证这一步也就是在验证所有分式在取此值时是否有意义;
信息2:遇到![]() 这种特征的题目,可以两边同时平方得到
这种特征的题目,可以两边同时平方得到![]() ;
;
信息3:遇到![]() 这种特征的题目,可以将左边变形,得到
这种特征的题目,可以将左边变形,得到![]() ,进而可以得到
,进而可以得到![]() 或
或![]() .
.
结合上述信息解决下面的问题:
问题1:如果![]() .可得:
.可得:![]() ;
;
问题2:解关于b的方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com