
【题目】已知:△ABC中,AB=AC,∠B=α.
(1)如图1,点D,E分别在边AB,AC上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N,求证:BD+CE=BC.需补充条件∠EMN=(用含α的式子表示)补充条件后并证明;
(2)把(1)中的条件改为点D,E分别在边BA、AC延长线上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N(如图2),并补充条件∠EMN=(用含α的式子表示),通过观察或测量,猜想线段BD,CE与BC之间满足的数量关系,并予以证明.
【答案】
(1)![]()
α
(2)![]()
α
【解析】解:(1)当∠EMN= ![]() α时,BD+CE=BC.
α时,BD+CE=BC.
理由:如图1所示:连接DM.
∵AB=AC,
∴∠B=∠C=α.
∵MN是DE的垂直平分线,
∴DN=NE,DM=EM.
在△MND和△MNE中, ,
,
∴△MND≌△MNE.
∴∠DMN=∠EMN= ![]() α.
α.
∴∠DME=α.
∵∠C+∠CEM=∠DMB+∠DME,∠C=∠DME=α,
∴∠DMB=∠CEM.
在△BDM和△CME中, ,
,
∴△BDM≌△CME.
∴BD=MC,EC=BM.
又∵MB+MC=BC,
∴BD+EC=BC.
2)当∠EMN= ![]() α时,BD=CE+BC.
α时,BD=CE+BC.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠DBM=∠MCE.
∵MN是DE的垂直平分线,
∴DN=NE,DM=EM.
在△MND和△MNE中, ,
,
∴△MND≌△MNE.
∴∠DMN=∠EMN= ![]() α.
α.
∴∠EMD=∠B=α
∵∠BMD+∠MDB=α,∠EMC+∠CMD=α,
∴∠EMC=∠MDB.
在△BDM和△CME中, ,
,
∴△BDM≌△CME.
∴BD=MC,EC=BM.
又∵MB+BC=MC,
∴EC+BC=BD.
(1)当∠EMN= ![]() α时,BD+CE=BC.连接DM.先证明∠DME=α.接下来证明∠DMB=∠CEM.然后依据AAS可证明△BDM≌△CME,然后由全等三角形的性质可证得BD=MC,EC=BM,结合条件MB+MC=BC,可证得问题的结论;(2)当∠EMN=
α时,BD+CE=BC.连接DM.先证明∠DME=α.接下来证明∠DMB=∠CEM.然后依据AAS可证明△BDM≌△CME,然后由全等三角形的性质可证得BD=MC,EC=BM,结合条件MB+MC=BC,可证得问题的结论;(2)当∠EMN= ![]() α时,BD=CE+BC.先证明∠DMN=∠EMN=
α时,BD=CE+BC.先证明∠DMN=∠EMN= ![]() α.从而得到∠EMD=∠B=α,接下来,依据等角的补角相等可证得∠DBM=∠MCE,然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC,然后依据AAS可证明△BDM≌△CME,由全等三角形的性质可得到BD=MC,EC=BM,结合MB+BC=MC可证得EC+BC=BD.
α.从而得到∠EMD=∠B=α,接下来,依据等角的补角相等可证得∠DBM=∠MCE,然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC,然后依据AAS可证明△BDM≌△CME,由全等三角形的性质可得到BD=MC,EC=BM,结合MB+BC=MC可证得EC+BC=BD.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABOC的顶点A在第二象限,顶点B在x轴上,顶点C在y轴上,若正方形ABOC的面积等于7,则点A的坐标是 . 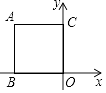
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有2个红球,1个黄球,它们除颜色外其余都相同.小丽和小亮做摸球游戏,约定游戏规则是:小丽先从袋中任意摸出1个球记下颜色后不放回,小亮再从袋中摸出1个球记下颜色,如果两人摸到的球的颜色相同则小丽赢,否则小亮赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( ) 
A.1
B.![]()
C.4﹣2 ![]()
D.3 ![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧. 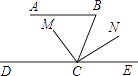
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车沿直路同向行驶,车速分别为20m/s和25m/s.现甲车在乙车前500m处,设xs(0≤x≤100)后两车相距ym.那么y关于x的数解析式为________(写出自变量取值范围)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com