Question

【题目】（1）如图①，分别以△ABC的边AB、AC为一边向形外作正方形ABDE和正方形ACGF．求证S△AEF＝S△ABC．

（2）如图②，分别以△ABC的边AB、AC、BC为边向形外作正方形ABDE、ACGF、BCHI，可得六边形DEFGHI，若S正方形ABDE＝17，S正方形ACGF＝25，S正方形BCHI＝16，求S六边形DEFGHI．

Answer 1

【答案】（1）证明见解析；（2）90.

【解析】

（1）过点C作CM⊥AB，过F作FN⊥EA与EA的延长线交于点N，求出∠CAM＝∠FAN，然后证明△AMC≌△ANF（AAS），得到CM＝FN，根据三角形面积公式可得结论；

（2）由（1）可得：S△AEF＝S△ABC＝S△BDI＝S△CHG，过点A作AO⊥BC于O，设BO＝x，则CO＝4x，根据勾股定理列方程得：17x2＝25（4x）2，解得x＝1，求出AO，根据面积和可得S六边形DEFGHI．

证明：（1）如图①，过点C作CM⊥AB，过F作FN⊥EA与EA的延长线交于点N，

∴∠CMA＝∠ANF＝90°，

∵四边形ABDE和四边形ACGF是正方形，

∴AB＝AE，AC＝AF，∠BAE＝∠BAN＝∠CAF＝90°，

∴∠CAM+∠CAN＝∠FAN+∠CAN＝90°，

∴∠CAM＝∠FAN，

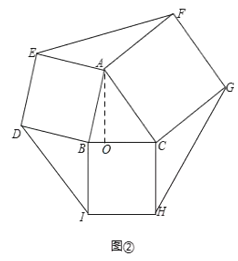
在△AMC和△ANF中，

∵，

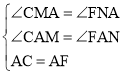∴△AMC≌△ANF（AAS），

∴CM＝FN，

∴AEFN＝，

∴S△AEF＝S△ABC；

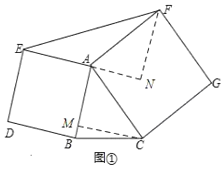
（2）由上题结论得：S△AEF＝S△ABC＝S△BDI＝S△CHG，

∵S正方形ABDE＝17，S正方形ACGF＝25，S正方形BCHI＝16，

∴AB＝，AC＝5，BC＝4，

过点A作AO⊥BC于O，设BO＝x，则CO＝4﹣x，

在Rt△ABO和Rt△ACO中，AO2＝AB2﹣BO2＝AC2﹣CO2，即17﹣x2＝25﹣（4﹣x）2，

解得：x＝1，即BO＝1，

∴，

S六边形DEFGHI＝S正方形ABDE+S正方形BCHI+S正方形ACGF+S△AEF+S△BDI+S△CHG+S△ABC，

＝17+25+16+4××4×4，

＝90．