有A、B、C、D、E五个队分在同一小组进行单循环足球比赛(每两队只进行一场比赛),为争夺出线权,比赛规则规定:胜一场得3分,平一场每队各得1分,负一场得0分,小组赛结束后,小组中名次在前的两个队出线,请你解答下列问题:
(1)小组赛结束后,若A队的积分为9分时,设A队胜x场,平y场,则3x+y=______,其中x,y为非负整数,且满足不等式x+y≤______,根据这些相等关系和不等关系,可以确定x=______,y=______.
(2)小组赛结束后,设5个队积分总和为n,则满足______≤n≤______.
(3)小组赛结束后,若A队的积分为10分,A队能出线吗?请你对A队能否出线做出分析.
解:(1)3x+y=9,x+y≤4,x=3,y=0;
(2)20≤n≤30,小组赛共10场比赛,全部平局总积分20分,
无平局时总积分n=10×3=30分;
(3)A队能出线.
若A队不能出线,则A队不在前两名,
那么前两名的积分都超过10分,
则前两名的积分与A队的积分总和超过了30分,这与题意不符,
所以A队是前两名,能出线.
故答案为:9,4,3,0;20,30.
分析:(1)根据A队的积分为9分,可得3x+y=9,由于每队进行4场足球比赛,可得x+y≤4,根据场次x,y为非负整数,解一元一次不等式组即可求解;
(2)由于两队比赛一场,两队总积分最多3分,最少2分,算出总的比赛场次,即可求解;
(3)利用反证法得出若A队不能出线,得出前两名的积分与A队的积分总和超过了30分,这与题意不符,从而求解.
点评:本题考查的是球类比赛的积分问题,只要弄清楚不同情况下场次和积分的不同关系就能顺利解答,有一定的难度.



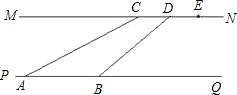 如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C、D、E…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110米到达B处,测得∠DBQ=45°,求河流的宽度.
如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C、D、E…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110米到达B处,测得∠DBQ=45°,求河流的宽度.