
【题目】如图所示,AB为半圆O的直径,C为圆上一点,AD平分∠BAC交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,DE= ![]() ,求线段AC的长
,求线段AC的长
【答案】
(1)证明:连接OD,
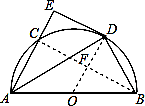
∵OA=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAD,
∴AE∥OD,
∴∠AED+∠EDO=180°,
∵DE⊥AC,
∴∠EDO=90°,
∴DE是⊙O的切线;
(2)解:连接BC交OD于F,
∵AB为直径,
∴∠ACB=90°,
∵∠AED=∠EDO=90°,
∴四边形DECF为矩形,
∴DE=CF= ![]() ,∠DFC=90°,
,∠DFC=90°,
∴OD⊥BC,
∴BC=2CF=2 ![]() ,
,
∵AB=4,
∴AC= ![]() =2.
=2.
【解析】(1)证切线需要证明该线垂直于过切点的半径,所以我们首先要连接OD,并进一步利用平行线性质,互补关系,证明∠EDO=90°
(2)利用垂径定理结合矩形性质可得DE=CF= ![]() ,BC=2CF=2
,BC=2CF=2 ![]() ,再利用勾股定理易得AC=
,再利用勾股定理易得AC= ![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:
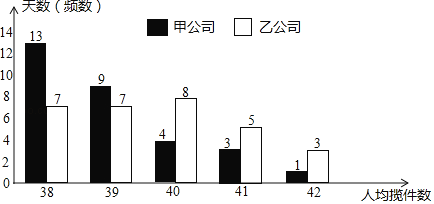
(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
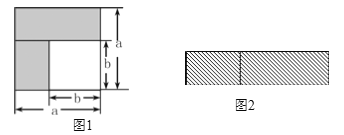
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
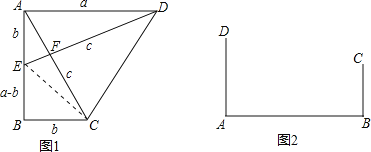
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com