
 (2013•莱芜)如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A、B上的观测点进行观测,从A岛测得渔船在南偏东37°方向C处,B岛在南偏东66°方向,从B岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A岛上维修船的速度为每小时20海里,B岛上维修船的速度为每小时28.8海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船?
(2013•莱芜)如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A、B上的观测点进行观测,从A岛测得渔船在南偏东37°方向C处,B岛在南偏东66°方向,从B岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A岛上维修船的速度为每小时20海里,B岛上维修船的速度为每小时28.8海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船?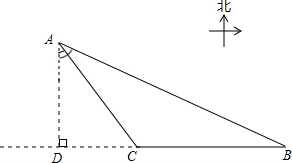 解:作AD⊥BC的延长线于点D.
解:作AD⊥BC的延长线于点D.| AD |
| cos∠DAC |
| 28.8 |
| cos37° |
| 28.8 |
| 0.8 |
| AC |
| 20 |
| 36 |
| 20 |
| BC |
| 28.8 |
| 43.2 |
| 28.8 |


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
 (2013•莱芜)如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( )
(2013•莱芜)如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(2013•莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com