
����Ŀ�������п�չ�����⡱��У�Ϊ����ѧ�����չ�����������ȫ�а��꼶����ͬѧ1���ӣ�����������У�����������������ͼ�������ͼ���ṩ��Ϣ��������⣺
��1�����ι���������ѧ����
��2���벹ȫֱ��ͼ��ȱ���֣�ֱ��д����ͼ�з�Χ135��x��155��������Բ�ĽǶ�����
��3�������γ���У���125�����ϣ���125�Σ�Ϊ���㣬�������ȫ��8000�����꼶ѧ�����ж�����ѧ���ɼ�Ϊ���㣿
��4���������������Ϣ�������п�չѧ���̸̸�Լ���������
���𰸡�
��1��
�⣺��������������8+16����12%=200���ˣ�
��2��
�⣺��Χ��115��x��145�������ǣ�200-8-16-71-60-16=29���ˣ���������������Χ135��x��155�������ε�Բ�ĽǶ����ǣ�360�� ![]() =81��
=81��
��3��
����ı����ǣ� ![]() ��100%=52.5%�������ȫ��8000�����꼶ѧ�����ж�����ѧ���ijɼ�Ϊ���������ǣ�8000��52.5%=4200���ˣ���
��100%=52.5%�������ȫ��8000�����꼶ѧ�����ж�����ѧ���ijɼ�Ϊ���������ǣ�8000��52.5%=4200���ˣ���
��4��
ȫ�дﵽ�����������һ�����ϣ���ӳ������ѧ����������ܺ�.�𰸲�Ψһ
����������1������95��x��115��������8+16=24�ˣ���ռ�ı�����12%������⣻��2����÷�Χ��115��x��145�����������ε�Բ�ĽǶ�����360�ȳ��Զ�Ӧ�ı���������⣻��3�����������ռ�ı�����Ȼ�����������8000������⣻��4������ʵ�����������Լ��ļ��⼴�ɣ��𰸲�Ψһ��


 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ж�����ijһ�������Ϊ��8�桫2�棬����һ����²��ǣ��� ����
A. 6��B. ��6��C. 10��D. ��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ�ú��ʵķ��������з���
��1����x+4��2=5��x+4������2����x+3��2=��1��2x��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ĶԽ����ཻ�ڵ�O����OҲ��������A��B��C��O��һ�����㣬���������εı߳�������1����������A��B��C��O�ƶ���Oת��ʱ�������������ص����ֵ������С��ʲô���ɣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε��ܳ�Ϊ13cm������һ�߳�Ϊ5cm����õ��������ε����߳�Ϊ_____cm.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н������о�ȷ��ǧλ���ǣ�������
A. 90200 B. 3.4��104 C. 3.450��102 D. 3.4��102
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��ֱ�߽�AD�ڵ�E����BC�ڵ�F������ABCD�����Ϊ30cm2������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F�ֱ���ABCD��AD��BC���ϵĵ㣬��AE=CF��
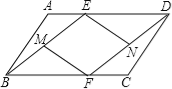
��1����֤����ABE�ա�CDF��
��2����M��N�ֱ���BE��DF���е㣬����MF��EN�����ж��ı���MFNE���������ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABOD�Ķ���A�Ǻ���y����x��(k��1)��ͼ���뺯��y��![]() �ڵڶ�����ͼ��Ľ��㣬B��D�������������ϣ��ҳ�����ABOD�����Ϊ3.
�ڵڶ�����ͼ��Ľ��㣬B��D�������������ϣ��ҳ�����ABOD�����Ϊ3.
(1)���������ı���ʽ��
(2)��������ͼ��Ľ���A��C�����ꣻ
(3)����P��y����һ���㣬��S��APC��5�����P�����꣮

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com