
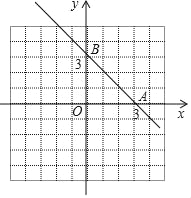
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B,与x轴的另一个交点为C,顶点为D.
(1)求抛物线的解析式;
(2)画出抛物线的图象;
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为y=﹣x2+2x+3.(2)图象见解析;(3)点N的坐标为(1,0)或(﹣7,0).
【解析】
(1)先求得点A和点B的坐标,然后将点A和点B的坐标代入抛物线的解析式求得b,c的值即可;
(2)依据抛物线解析式为y=-x2+2x+3,列表,描点,连线即可;
(3)先利用配方法求得点D的坐标,当∠DNA=90°时,DN⊥OA,可得到点N的坐标,从而得到AN=2,然后再求得AD的长;当∠N′DA=90°时,依据sin∠DN′A=sin∠ADN可求得AN′的长,从而可得到N′的坐标.
解:(1)将x=0代入AB的解析式y=﹣x+3得:y=3,
∴B(0,3).
将y=0代入AB的解析式y=﹣x+3得:﹣x+3=0,
解得x=3,
即A(3,0).
将点A和点B的坐标代入y=﹣x2+bx+c,得:
![]() ,
,
解得:b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)列表:
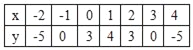
抛物线的图象如下:
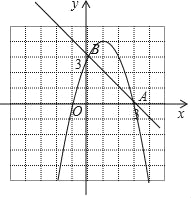
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
①当∠DNA=90°时,如图所示:
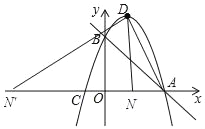
∵∠DNA=90°时,
∴DN⊥OA.
又∵D(1,4)
∴N(1,0).
∴AN=2.
∵DN=4,AN=2,
∴AD=2![]() .
.
②当∠N′DA=90°时,则∠DN′A=∠NDA.
∴![]() ,
,
即![]() ,
,
解得:AN′=10.
∵A(3,0),
∴N′(﹣7,0).
综上所述,点N的坐标为(1,0)或(﹣7,0).


科目:初中数学 来源: 题型:
【题目】如图1,笔直的公路上有A、B两个站点相距40km,在公路的同侧有C、D两个村庄,DA⊥AB,CB⊥AB,且DA=20km,CB=10km,现政府决定在A、B之间建一个土特产加工基地E.
(1)若要使土特产加工基地E点到C、D两村的距离相等,请用直尺和圆规在图1中作出点E;
(2)在(1)的条件下求出基地E到A站的距离;
(3)若要使土特产加工基地E点到C、D两村的距离和(即DE +EC)最小,求出此最小的距离和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 月初,西雅中学初二年级前往距离学校
月初,西雅中学初二年级前往距离学校![]() 的莲花镇基地研学.学生乘坐大巴,刘老师自行驾车前往,已知刘老师自行驾车的速度是大巴速度的
的莲花镇基地研学.学生乘坐大巴,刘老师自行驾车前往,已知刘老师自行驾车的速度是大巴速度的![]() 倍,他们同时从学校出发,结果刘老师比学生早
倍,他们同时从学校出发,结果刘老师比学生早![]() 到达目的地,
到达目的地,
(1)求大巴的速度;
(2)如果刘老师到基地后不停留,直接驾车到离基地![]() 的药店购买常用药以备不时之需,再赶回基地,其中在药店买药用时
的药店购买常用药以备不时之需,再赶回基地,其中在药店买药用时![]() 分钟.请问刘老师能在大巴到达之前赶回基地吗?
分钟.请问刘老师能在大巴到达之前赶回基地吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
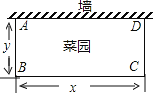
A. y=-2x+24(0<x<12) B. y=-![]() x+12(0<x<24)
x+12(0<x<24)
C. y=2x-24(0<x<12) D. y=![]() x-12(0<x<24)
x-12(0<x<24)
查看答案和解析>>
科目:初中数学 来源: 题型:
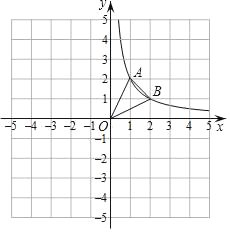
【题目】如图,反比例函数![]() (k≠0)的图象经过点A(1,2)和B(2,n),
(k≠0)的图象经过点A(1,2)和B(2,n),
(1)以原点O为位似中心画出△A1B1O,使![]() =
=![]() ;
;
(2)在y轴上是否存在点P,使得PA+PB的值最小?若存在,求出P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:如调整价格,每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,如何定价才能使利润最大?这个最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
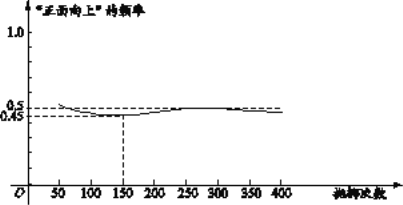
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com