
分析 (1)设一次函数解析式为y=kx+b,把A坐标代入求出b的值,把B与C坐标代入求出k的值,即可确定出解析式;
(2)对于一次函数解析式,令y=0求出x的值,确定出D坐标,进而表示出OD的长,P纵坐标为OD边上的高,利用三角形面积公式表示出S与x的关系式即可;
(3)令S=1,求出x的值即可.
解答 解:(1)设一次函数解析式为y=kx+b,
把A(0,-3)代入得:b=-3,
把B与C坐标代入得:$\left\{\begin{array}{l}{k-3=a}\\{ak-3=1}\end{array}\right.$,
解得:k=4或k=-1,
∵函数值y随着x的值增大而增大,
∴k=4,
则一次函数解析式为y=4x-3;
(2)对于一次函数y=4x-3,令y=0,得到x=$\frac{3}{4}$,即D($\frac{3}{4}$,0),
则S△POD=$\frac{1}{2}$×$\frac{3}{4}$(4x-3)=$\frac{3}{2}$x-$\frac{9}{8}$(x>0);
(3)令S=1,得到$\frac{3}{2}$x-$\frac{9}{8}$=1,
解得:x=$\frac{17}{12}$.
点评 此题考查了待定系数法求一次函数解析式,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:填空题
 如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD=$\frac{6}{5}$或$\frac{4}{3}$.
如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD=$\frac{6}{5}$或$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
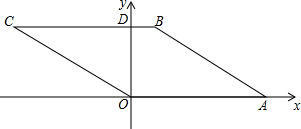 如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )
如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 受台风影响,一棵大树从B处被折断,树的顶部落在离树根底部C相距4米的A处,测得∠CAB=60°,那么这棵树折断前高为14.9米$(结果保留一位小数,\sqrt{3}≈1.73)$.
受台风影响,一棵大树从B处被折断,树的顶部落在离树根底部C相距4米的A处,测得∠CAB=60°,那么这棵树折断前高为14.9米$(结果保留一位小数,\sqrt{3}≈1.73)$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 34℃~38℃ | B. | 35℃~37℃ | C. | 34℃~35℃ | D. | 37℃~38℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com