
如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论的个数有( )个.

A.5??????? B.4??????? C.3?????? D.2
B.
【解析】
试题分析:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵在△APE和△AME中,
 ,
,
∴△APE≌△AME,故①正确;
∴PE=EM= PM,
PM,
同理,FP=FN= NP.
NP.
∵正方形ABCD中AC⊥BD,
又∵PE⊥AC,PF⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,且△APE中AE=PE
∴四边形PEOF是矩形.
∴PF=OE,
∴PE+PF=OA,
又∵PE=EM= PM,FP=FN=
PM,FP=FN= NP,OA=
NP,OA= AC,
AC,
∴PM+PN=AC,故②正确;
∵四边形PEOF是矩形,
∴PE=OF,
在直角△OPF中,OF2+PF2=PO2,
∴PE2+PF2=PO2,故③正确.
∵△BNF是等腰直角三角形,而△POF不一定是,故④错误;
∵△AMP是等腰直角三角形,当△PMN∽△AMP时,△PMN是等腰直角三角形.
∴PM=PN,
又∵△AMP和△BPN都是等腰直角三角形,
∴AP=BP,即P时AB的中点.故⑤正确.
故选B.
考点: 1.相似三角形的判定与性质;2.全等三角形的判定与性质;3.勾股定理;4.正方形的性质.


科目:初中数学 来源: 题型:
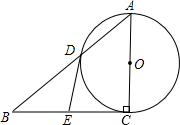 ,交BC于点E.
,交BC于点E.| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
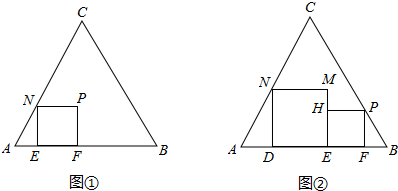
查看答案和解析>>
科目:初中数学 来源: 题型:
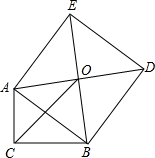 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com