
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,它们离甲地的路程y(km)与客车行驶时间x(h)间的函数关系如图,下列信息:
(1)出租车的速度为100千米/时;
(2)客车的速度为60千米/时;
(3)两车相遇时,客车行驶了3.75小时;
(4)相遇时,出租车离甲地的路程为225千米.
其中正确的个数有( )
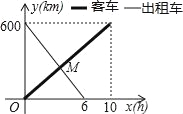
A. 1个 B. 2个 C. 3个 D. 4个
科目:初中数学 来源: 题型:
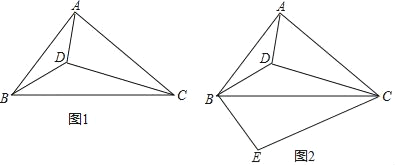
【题目】如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若ACBD=ADBC,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
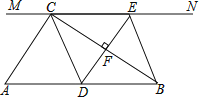
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由.
(2)在(1)的条件下,当∠A=__________°时,四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015山东省德州市,24,12分)已知抛物线y=-mx2+4x+2m与x轴交于点A(α,0), B(β,0),且![]() .
.
(1)求抛物线的解析式.
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E.是否存在x轴上的点M、y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弧CD⊥AB,垂足为H,P为弧AD上一点,连接PA、PB,PB交CD于E.
(1)如图(1)连接PC、CB,求证:∠BCP=∠PED;
(2)如图(2)过点P作⊙O的切线交CD的延长线于点E,过点A向PF引垂线,垂足为G,求证:∠APG=![]() ∠F;
∠F;
(3)如图(3)在图(2)的条件下,连接PH,若PH=PF,3PF=5PG,BE=2![]() ,求⊙O的直径AB.
,求⊙O的直径AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.

查看答案和解析>>
科目:初中数学 来源: 题型:
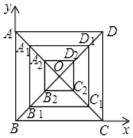
【题目】如图以正方形ABCD的B点为坐标原点.BC所在直线为x轴,BA所在直线为y轴,建立直角坐标系.设正方形ABCD的边长为6,顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1,得到正方形A1B1C1D1,再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2.按以上方法依次得到正方形A1B1C1D1,……AnBnCnDn,(n为不小于1的自然数),设An点的坐标为(xn,yn),则xn+yn=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
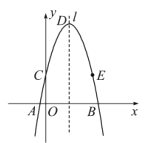
【题目】已知:已知二次函数的图象与![]() 轴交于
轴交于![]() 和
和![]() 两点.交
两点.交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是二次函数图象上的一对对称点,一次函数的图象过点
是二次函数图象上的一对对称点,一次函数的图象过点![]() ,
,![]()
(1)画出图象,并求二次函数的解析式.
(2)根据图象直接写出使一次函数值大于或等于二次函数值的![]() 的取值范围.
的取值范围.
(3)若直线与![]() 轴交点为
轴交点为![]() ,连接
,连接![]() ,
,![]() ,求三角形
,求三角形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com