
【题目】如图,在平面直角坐标系中,四边形OABC四个顶点的坐标分别为O(0,0),A(﹣3,0),B(﹣4,2),C(﹣1,2).将四边形OABC绕点O顺时针旋转90°后,点A,B,C分别落在点A′,B′,C′处. 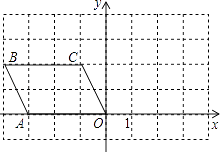
(1)请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′;
(2)点C旋转到点C′所经过的弧的半径是 , 点C经过的路线长是 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
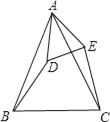
【题目】如图,△ABC和△ADE都是等腰三角形,BC、DE分别是这两个等腰三角形的底边,且∠BAC=∠DAE.
(1)求证:BD=CE;
(2)连接DC.如果CD=CE,试说明直线AD垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】8筐白菜,以每25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)这8筐白菜中最接近标准重量的这筐白菜重______ 千克;
(2)与标准重量比较,8筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这8筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种笔记本的售价为2.2元/本,如果买100本以上,超过100本部分的售价为2元/本.
(1)小强和小明分别买了50本和200本,他们俩分别花了多少钱?
(2)如果小红买这种笔记本花了380元,她买了多少本?
(3)如果小红买这种笔记本花了n元,她又买了多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图像可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图像,可以得到不等式ax+b> ![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.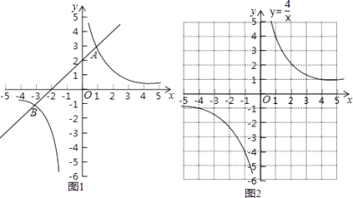
下面是他的探究过程,请将(1)、(2)、(3)补充完整:
(1)①将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1<![]() ;
;
②构造函数,画出图像
设y3=x2+4x﹣1,y4=![]() , 在同一坐标系中分别画出这两个函数的图像.
, 在同一坐标系中分别画出这两个函数的图像.
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(2)确定两个函数图像公共点的横坐标
观察所画两个函数的图像,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为
(3)借助图像,写出解集
结合(1)的讨论结果,观察两个函数的图像可知:不等式x3+4x2﹣x﹣4>0的解集为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”(jiǒng)是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为8cm的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为xcm、ycm,剪去的两个小直角三角形的两直角边长也分别为xcm、ycm.

(1)用含有x、y的代数式表示图中“囧”(阴影部分)的面积.
(2)当x=8,y=2时,求此时“囧”(阴影部分)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点. 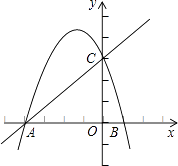
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=12 cm,BC=6 cm.点P沿AB边从点A开始向点B以2 cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.


设点P,Q同时出发,用t(s)表示移动的时间.
(发现) DQ=________cm,AP=________cm.(用含t的代数式表示)
(拓展)(1)如图①,当t=________s时,线段AQ与线段AP相等?
(2)如图②,点P,Q分别到达B,A后继续运动,点P到达点C后都停止运动.
当t为何值时,AQ=![]() CP?
CP?
(探究)若点P,Q分别到达点B,A后继续沿着A—B—C—D—A的方向运动,当点P与点Q第一次相遇时,请直接写出相遇点的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com