
【题目】我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.如图,在平面直角坐标系xOy中,已知抛物线y=x2﹣2x,其顶点为A.
(1)试求抛物线y=x2﹣2x的“不动点”的坐标;
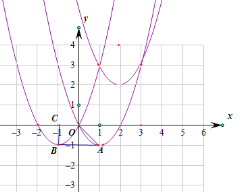
(2)平移抛物线y=x2﹣2x,使所得新抛物线的顶点B是该抛物线的“不动点”,其对称轴与x轴交于点C,且四边形OABC是梯形,求新抛物线的表达式.
【答案】(1)抛物线的“不动点”为(0,0),(3,3);(2)新抛物线的解析式为y=x2+2x
【解析】
(1)设抛物线y=x2﹣2x的“不动点”的坐标(t,t),则t=t2﹣2t,求得t=0或t=3;
(2)OC∥AB时,设B(m,m),则新抛物线的对称轴为x=m,与x轴的交点C(m,0),当OC∥AB,由A(1,﹣1),B(m,m),可求m=﹣1,故新抛物线是抛物线y=x2﹣2x向左平移2个单位得到的;当OB∥AC时,同理可得:抛物线解析式y=﹣(x﹣2)2+2=x2﹣4x+6,当四边形OABC是梯形,字母顺序不对,故舍去;
解:(1)设抛物线y=x2﹣2x的“不动点”的坐标(t,t),
则t=t2﹣2t,
∴t=0或t=3,
∴抛物线的“不动点”为(0,0),(3,3);
(2)当OC∥AB时,
∵新抛物线顶点B为“不动点”,则设点B(m,m),
∴新抛物线的对称轴为:x=m,与x轴的交点C(m,0),
∵四边形OABC是梯形,
∴直线x=m在y轴左侧,
∵BC与OA不平行,
∴OC∥AB,
又∵点A(1,-1),点B(m,m),
∴m=-1,
故新抛物线是由抛物线y=x2-2x向左平移2个单位得到的,
∵原抛物线y=x2﹣2x=(x-1)2-1,
∴平移后的抛物线为:y=(x+1)2-1=x2+2x;
当OB∥AC时,
同理可得:抛物线的表达式为:y=(x-2)2+2=x2-4x+6,
当四边形OABC是梯形,字母顺序不对,故舍去,
综上,新抛物线的表达式为:y= x2+2x.
综上所述:新抛物线的解析式为y=x2+2x.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
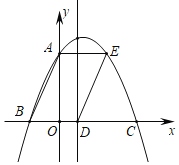
【题目】如图,抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
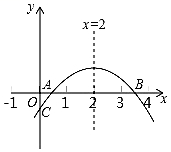
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交于A、B两点,与
轴正半轴相交于A、B两点,与![]() 轴相交于点C,对称轴为直线
轴相交于点C,对称轴为直线![]() 且OA=OC,则下列结论:①
且OA=OC,则下列结论:①![]() ②
②![]() ③
③![]() ④关于
④关于![]() 的方程
的方程![]() 有一个根为
有一个根为![]() 其中正确的结论个数有( )
其中正确的结论个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研制出新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元,但最低销售单价为2600元。请解决下列问题:
(1)直接写出:购买这种产品 ________件时,销售单价恰好为2600元;
(2)设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,求y与x之间的函数表达式;
(3)该公司的销售人员发现:当购买产品的件数超过10件时,会出现随着数量的增多,公司所获利润反而减少这一情况.为使购买数量越多,公司所获利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副扑克牌中点数为“2”、“3”、“4”、“6”的四张牌背面朝上洗匀,先从中抽出1张牌,记录下牌面点数为x,再从余下的3张牌中抽出1张牌,记录下牌面点数为y.设点P的坐标为(x,y).
(1)请用表格或树状图列出点P所有可能的坐标.
(2)求点P在抛物线y=x2+x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
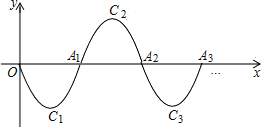
【题目】如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0B.﹣![]() C.2D.﹣2
C.2D.﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示1,现将点
表示1,现将点![]() 沿
沿![]() 轴做如下移动,第一次点
轴做如下移动,第一次点![]() 向左移动3个单位长度到达点
向左移动3个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动6个单位长度到达点
向右移动6个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离不小于20,那么
与原点的距离不小于20,那么![]() 的最小值是__________.
的最小值是__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=k1x(k1≠0)与反比例函数![]() 的图象交于A、B两点,点A的坐标为(2,1).
的图象交于A、B两点,点A的坐标为(2,1).
(1)求正比例函数、反比例函数的表达式;
(2)求点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com