
【题目】已知抛物线的解析式为y=x2﹣(2m﹣1)x+m2﹣m.
(1)请说明此抛物线与x轴的交点情况;
(2)若此抛物线与直线y=x﹣3m+4的一个交点在y轴上,求m的值.
【答案】
(1)解:△=[﹣(2m﹣1)]2﹣4×(m2﹣m)=4m2﹣4m+1﹣4m2+4m=1>0,
所以抛物线与x轴有两个不相同的交点
(2)解:当x=0时,可得m2﹣m=﹣3m+4,
整理得,m2+2m﹣4=0,
解得,m1=﹣1 ![]() ,m2=﹣1﹣
,m2=﹣1﹣ ![]()
【解析】(1)利用一元二次方程根的判别式判断即可;(2)根据题意列出方程,解方程即可.
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过点A(4,0),C(0,﹣4),另有一点B(﹣2,0).
(1)求一次函数解析式;
(2)联结BC,点P是反比例函数y= ![]() 的第一象限图象上一点,过点P作y轴的垂线PQ,垂足为Q.如果△QPO与△BCO相似,求P点坐标;
的第一象限图象上一点,过点P作y轴的垂线PQ,垂足为Q.如果△QPO与△BCO相似,求P点坐标;
(3)联结AC,求∠ACB的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1 . 使得点P1与点O关于点A成中心对称;第二次跳跃到点P2 , 使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3 , 使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4 , 使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5 , 使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是 , 点P2016的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=﹣x2+bx+c经过A(0,﹣2),B(﹣1,1)两点,那么此抛物线经过( )
A.第一、二、三、四象限
B.第一、二、三象限
C.第一、二、四象限
D.第二、三、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施“农业立市,工业强市,旅游兴市”计划后,2009年全市荔枝种植面积为24万亩.调查分析结果显示.从2009年开始,该市荔枝种植面积y(万亩)随着时间x(年)逐年成直线上升,y与x之间的函数关系如图所示. 
(1)求y与x之间的函数关系式(不必注明自变量x的取值范围);
(2)该市2012年荔枝种植面积为多少万亩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么当再过多长时间轮船离灯塔最近?( )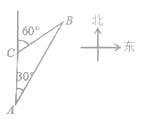
A.1小时
B.![]()
小时
C.2小时
D.2 ![]() 小时
小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com