
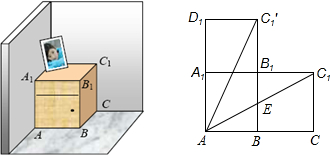
 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.小明认为蚂蚁能够最快到达目的地的路径AC1,小王认为蚂蚁能够最快到达目的地的路径AC1′.已知AB=4,BC=4,CC1=5时,请你帮忙他们求出蚂蚁爬过的最短路径长.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.小明认为蚂蚁能够最快到达目的地的路径AC1,小王认为蚂蚁能够最快到达目的地的路径AC1′.已知AB=4,BC=4,CC1=5时,请你帮忙他们求出蚂蚁爬过的最短路径长.科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
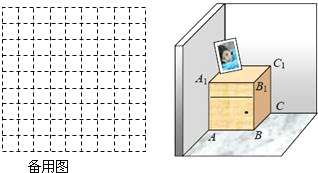 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.若AB=4,BC=4,CC1=5,
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.若AB=4,BC=4,CC1=5,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.查看答案和解析>>
科目:初中数学 来源:2011-2012年福建省泉州市永春县八年级上册期中考试数学试卷(解析版) 题型:解答题
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.小明认为蚂蚁能够最快到达目的地的路径AC1,小王认为蚂蚁能够最快到达目的地的路径AC1′.已知AB=4,BC=4,CC1=5时,请你帮忙他们求出蚂蚁爬过的最短路径的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com