
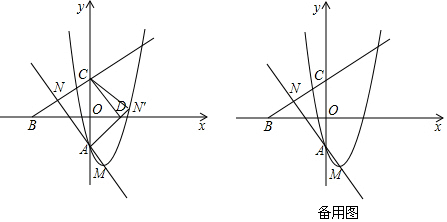
ЗжЮі ЃЈ1ЃЉвбжЊСЫХзЮяЯпЕФНтЮіЪНЃЌВЛФбгУЙЋЪНЗЈЧѓГіMЕФзјБъЮЊЃЈ1ЃЌ-a-1ЃЉЃЎгЩгкХзЮяЯпЙ§AЕуЃЌвђДЫAЕФзјБъЪЧЃЈ0ЃЌ-aЃЉЃЎИљОнAЃЌMЕФзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈПЩЕУГіжБЯпAMЕФНтЮіЪНЮЊy=-x-aЃЎжБЯпAMКЭy=$\frac{1}{2}$x+aСЊСЂЗНГЬзщМДПЩЧѓГіNЕФзјБъЃЎ
ЃЈ2ЃЉИљОнелЕўЕФаджЪВЛФбЕУГіNгыNЁфе§КУЙигкyжсЖдГЦЃЌЕУГіNЁфЕФзјБъЃЎгЩгкNЁфдкХзЮяЯпЩЯЃЌвђДЫНЋNЁфЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНжаМДПЩЕУГіaЕФжЕЃЎвВОЭФмШЗЖЈNЃЌCЕФзјБъЃЎЧѓГіЁїANCКЭЁїADCЕФУцЛ§ЃЌМДПЩЕУГіЁїCDNЕФУцЛ§ЃЛ
ЃЈ3ЃЉБОЬтПЩЗжСНжжЧщПіНјааЬжТлЃК
ЂйЕБPдкyжсзѓВрЪБЃЌШчЙћЪЙвдPЃЌNЃЌAЃЌCЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌФЧУДPашвЊТњзуЕФЬѕМўЪЧPNЦНааЧвЯрЕШгкACЃЌвВОЭЪЧЫЕЃЌШчЙћNЕуЯђЩЯЦНвЦACИіЕЅЮЛМД2aКѓЕУЕНЕФЕуОЭЪЧPЕуЃЎШЛКѓНЋДЫЪБPЕФзјБъДњШыХзЮяЯпжаЃЌШчЙћУЛгаНтЫЕУїВЛДцдкетбљЕФЕуPЃЌШчЙћФмЧѓГіaЕФжЕЃЌФЧУДМДПЩЧѓГіДЫЪБPЕФзјБъЃЎ
ЂкЕБPдкyжсгвВрЪБЃЌPашвЊТњзуЕФЬѕМўЪЧPNгыACгІЛЅЯрЦНЗжЃЈЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗжЃЉЃЌФЧУДNPБиЙ§дЕуЃЌЧвЙигкдЕуЖдГЦЃЎФЧУДПЩЕУГіДЫЪБPЕФзјБъЃЌШЛКѓДњШыХзЮяЯпЕФНтЮіЪНжаАДЂйЕФЗНЗЈЧѓНтМДПЩЃЎ
НтД№  НтЃКЃЈ1ЃЉMЃЈ1ЃЌ-a-1ЃЉЃЌNЃЈ-$\frac{4}{3}$aЃЌ$\frac{1}{3}$aЃЉЃЛ
НтЃКЃЈ1ЃЉMЃЈ1ЃЌ-a-1ЃЉЃЌNЃЈ-$\frac{4}{3}$aЃЌ$\frac{1}{3}$aЃЉЃЛ
ЙЪД№АИЮЊЃК1ЃЌ-a-1ЃЛ-$\frac{4}{3}$aЃЌ$\frac{1}{3}$aЃЛ
ЃЈ2ЃЉЁпгЩЬтвтЕУЕуNгыЕуNЁфЙигкyжсЖдГЦЃЌ
ЁрNЁфЃЈ$\frac{4}{3}$aЃЌ$\frac{1}{3}$aЃЉЃЎ
НЋNЁфЕФзјБъДњШыy=x2-2x-aЕУЃК$\frac{1}{3}$a=$\frac{16}{9}$a2-$\frac{8}{3}$a-aЃЌ
Ёрa1=0ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌa2=$\frac{9}{4}$ЃЎ
ЁрNЃЈ-3ЃЌ$\frac{3}{4}$ЃЉЃЌ
ЁрЕуNЕНyжсЕФОрРыЮЊ3ЃЎ
ЁпAЃЈ0ЃЌ-$\frac{9}{4}$ЃЉЃЌN'ЃЈ3ЃЌ$\frac{3}{4}$ЃЉЃЌ
ЁржБЯпAN'ЕФНтЮіЪНЮЊy=x-$\frac{9}{4}$ЃЌЫќгыxжсЕФНЛЕуЮЊDЃЈ$\frac{9}{4}$ЃЌ0ЃЉЃЌ
ЁрЕуDЕНyжсЕФОрРыЮЊ$\frac{9}{4}$ЃЎ
гЩЬтжЊЃЌAЃЈ0ЃЌaЃЉЃЌCЃЈ0ЃЌ-aЃЉЃЌ
ЁрЕуAЃЌCЙигкxжсЖдГЦЃЌ
ЁрAC=2AOЃЌ
ЁрSЁїCDN=SЁїACN-SЁїACD=$\frac{1}{2}$ЁС$\frac{9}{2}$ЁС3-$\frac{1}{2}$ЁС$\frac{9}{2}$ЁС$\frac{9}{4}$=$\frac{27}{16}$ЃЛ
ЃЈ3ЃЉДцдкЃЌРэгЩШчЯТЃК
ЂйЕБЕуPдкyжсЕФзѓВрЪБЃЌШєЫФБпаЮACPNЪЧЦНааЫФБпаЮЃЌ
дђPNЁЮACЃЌPN=ACЃЌ
дђАбNЯђЩЯЦНвЦ2aИіЕЅЮЛЕУЕНPЃЌзјБъЮЊЃЈ-$\frac{4}{3}$aЃЌ$\frac{7}{3}$aЃЉЃЌ
ДњШыХзЮяЯпЕФНтЮіЪНЃЌЕУЃК$\frac{7}{3}$a=$\frac{16}{9}$a2+$\frac{8}{3}$a-aЃЌ
НтЕУa1=0ЃЈВЛЩсЬтвтЃЌЩсШЅЃЉЃЌa2=$\frac{3}{8}$ЃЌ
дђPЃЈ-$\frac{1}{2}$ЃЌ$\frac{7}{8}$ЃЉЃЛ
ЂкЕБЕуPдкyжсЕФгвВрЪБЃЌШєЫФБпаЮAPCNЪЧЦНааЫФБпаЮЃЌдђACгыPNЛЅЯрЦНЗжЃЌ
дђOA=OCЃЌOP=ONЃЎ
дђPгыNЙигкдЕуЖдГЦЃЌдђPЃЈ$\frac{4}{3}$aЃЌ-$\frac{1}{3}$aЃЉЃЛ
НЋPЕузјБъДњШыХзЮяЯпНтЮіЪНЕУЃК-$\frac{1}{3}$a=$\frac{16}{9}$a2-$\frac{8}{3}$a-aЃЌ
НтЕУa1=0ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌa2=$\frac{15}{8}$ЃЌ
дђPЃЈ$\frac{5}{2}$ЃЌ-$\frac{5}{8}$ЃЉЃЎ
ЙЪДцдкетбљЕФЕуPЃЈ-$\frac{1}{2}$ЃЌ$\frac{7}{8}$ЃЉЛђPЃЈ$\frac{5}{2}$ЃЌ-$\frac{5}{8}$ЃЉЃЌФмЪЙЕУвдPЃЌAЃЌCЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ЕуЦР БОЬтЪЧЖўДЮКЏЪ§злКЯЬтФПЃЌзХжиПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЁЂЭМаЮа§зЊБфЛЛЁЂЦНааЫФБпаЮЕФаджЪЕШживЊжЊЪЖЕуЃЌзлКЯадЧПЃЌФмСІвЊЧѓНЯИпЃЎПМВщбЇЩњЗжРрЬжТлЃЌЪ§аЮНсКЯЕФЪ§бЇЫМЯыЗНЗЈЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌвЛИізЊХЬБЛЗжГЩ3ЕШЗжЃЌУПвЛЗнЩЯИїаДгавЛИіЪ§зжЃЌЫцЛњзЊЖЏзЊХЬ2ДЮЃЌЕквЛДЮзЊЕНЕФЪ§зжЪ§зжЮЊЪЎЮЛЪ§зжЃЌЕкЖўДЮзЊЕНЕФЪ§зжЮЊИіЮЛЪ§зжЃЌ2ДЮзЊЖЏКѓзщГЩвЛИіСНЮЛЪ§ЃЈШєжИеыЭЃдкЕШЗжЯпЩЯдђжиаТзЊвЛДЮЃЉ
ШчЭМЃЌвЛИізЊХЬБЛЗжГЩ3ЕШЗжЃЌУПвЛЗнЩЯИїаДгавЛИіЪ§зжЃЌЫцЛњзЊЖЏзЊХЬ2ДЮЃЌЕквЛДЮзЊЕНЕФЪ§зжЪ§зжЮЊЪЎЮЛЪ§зжЃЌЕкЖўДЮзЊЕНЕФЪ§зжЮЊИіЮЛЪ§зжЃЌ2ДЮзЊЖЏКѓзщГЩвЛИіСНЮЛЪ§ЃЈШєжИеыЭЃдкЕШЗжЯпЩЯдђжиаТзЊвЛДЮЃЉВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌвбжЊжБЯпABКЭCDЯрНЛгкЕуOЃЌЩфЯпOEЁЭABгкЕуOЃЌЩфЯпOFЁЭCDгкЕуOЃЌЧвЁЯBOF=50ЁуЃЌЧѓЁЯAOCКЭЁЯEODЕФЖШЪ§ЃЎ
ШчЭМЃЌвбжЊжБЯпABКЭCDЯрНЛгкЕуOЃЌЩфЯпOEЁЭABгкЕуOЃЌЩфЯпOFЁЭCDгкЕуOЃЌЧвЁЯBOF=50ЁуЃЌЧѓЁЯAOCКЭЁЯEODЕФЖШЪ§ЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com