
| A. | 正方形 | B. | 正六边形 | C. | 正八边形 | D. | 正三角形 |
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{3x}$ | C. | $\root{3}{9}$ | D. | $\sqrt{2x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=4x2-4ax+a2-2a+2,
已知二次函数y=4x2-4ax+a2-2a+2,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | 5 | C. | 2 | D. | 不存在 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 收费方式 | 月使用费(元) | 包月上网时间(h) | 超时费(元/h) |
| A | 7 | 25 | 3.6 |
| B | 10 | 50 | 4.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、三、四象限 | D. | 第一、二、三象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
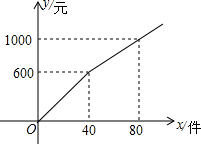 梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系图象如图所示,则降价后每件商品的销售利润为( )
梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系图象如图所示,则降价后每件商品的销售利润为( )| A. | 4元 | B. | 5元 | C. | 10元 | D. | 15元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com